В задачах моделирования динамических систем наиболее часто приходится решать дифференциальные уравнения второго порядка.
Общий вид дифференциальных уравнений второго порядка:

| (12.10) |
Нормальная форма дифференциальных уравнений второго порядка:

| (12.11) |
Пример
Уравнение в общем виде

Его нормальная форма

| (12.12) |
Дифференциальное уравнение второго порядка (12.11) можно свести к системе, состоящей из двух дифференциальных уравнений первого порядка при помощи замен.
Заменим y1=y',
Тогда y'1=y".
В результате уравнение (12.11) сводится к системе, состоящей из двух дифференциальных уравнений первого порядка:

Для примера (12.12) эта система имеет вид:

| (12.13) |
Решением этой системы являются две функции y(x) и y1(x),
где

Сформулируем задачу Коши для системы, состоящей из двух дифференциальных уравнений второго порядка.
Дана система

| (12.14) |
Даны два начальных условия:

Необходимо проинтегрировать систему на участке [a, b] с шагом h.
В численных методах задача Коши для системы (12.14) ставится следующим образом:
Найти табличные функции
 и
и  т.е. найти таблицу
т.е. найти таблицу
| i | x | y | y1 |
| 0 | x0 | y0 | (y1)0 |
| 1 | x1 | y1 | (y1)1 |
| 2 | x2 | y2 | (y1)2 |
| 3 | x3 | y3 | (y1)3 |
| ... | ... | ... | ... |
| n | xn | yn | (y1)n |
Здесь
h - шаг интегрирования дифференциального уравнения,
a=x0 - начало участка интегрирования уравнения,
b=xn - конец участка,
n=(b-a)/h - число шагов интегрирования уравнения.
На графике решением задачи Коши для системы, состоящей из двух дифференциальных уравнений первого порядка, является совокупность узловых точек (рис. 12.15).
При этом на каждом шаге, т.е. для каждого значения xi решением являются две узловые точки с координатами (xi, yi), (xi, (y1)i).

Рис. 12.15.
Для решения системы дифференциальных уравнений используем те же методы, что и для решения одного дифференциального уравнения первого порядка. При этом необходимо соблюдать условие: на каждом шаге интегрирования, т. е. в точках с координатами х1, х2, х3,:, хn все уравнения системы надо решать параллельно.
Для вычисления правых частей уравнений системы (12.14) необходимо сформировать подпрограмму PRAV.
Вернемся к примеру (12.13). Здесь на каждом шаге в подпрограмме PRAV будем вычислять правые части каждого уравнения системы:
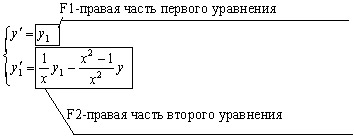
Схема алгоритма решения системы (12.13) представлена на рис 12.16.

Рис. 12.16. Схема алгоритма решения системы (12.6)
Здесь
h - шаг интегрирования дифференциального уравнения,
b - конец участка,
n - число шагов интегрирования уравнения,
x, y, y1 - при вводе начальные значения, далее - текущие значения табличной функции.
Решение дифференциальных уравнений m-го порядка методом Рунге-Кутта (4-го порядка)
Как уже было сказано, любое дифференциальное уравнение m-го порядка

| (12.15) |
сводится к системе, состоящей из m дифференциальных уравнений 1-го порядка

| (12.6) |
Численным решением системы (12.9), а значит и дифференциального уравнения m-го порядка (12.8) является m табличных функций

т.е. функция y(x) и все ее производные, включая производную (m-1)-го порядка.
При этом каждая из табличных функций определяется на промежутке [a, b] с шагом h и включает n узловых точек. Таким образом, численным решением уравнения (12.8) или системы (12.9) является матрица порядка  , (табл. 12.8)
, (табл. 12.8)
Таблица 12.1.





 , соответствуют m узловых точек скоординатами
, соответствуют m узловых точек скоординатами

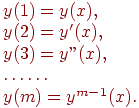




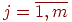 ;
; 

 ).
).

