Лекция 12. Компьютерное моделирование и решение нелинейных уравнений

Динамические системы - это системы, в которых входные переменные являются функциями от времени или каких-либо других параметров. Описываются эти системы дифференциальными и интегральными уравнениями. Например, большая часть законов механики, электротехники, теории упругости, теории управления и т.д. описываются с помощью дифференциальных уравнений.

На практике динамические системы встречаются очень часто. Моделирование систем, связанных с движением тел, с расчетом потоков энергии, с расчетом потоков материальных ресурсов, с расчетом оборотов денежных средств и т.д. в конечном счете, сводится к построению и решению дифференциальных уравнений (как правило, II-го порядка).

Прямолинейное движение тела, движущегося под действием переменной силы ,где S=S(t), описывается дифференциальным уравнением второго порядка в форме уравнения Ньютона:

где

m - масса тела,

S - перемещение тела,

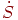-линейная скорость,

-линейное ускорение.

При этом задаваемые начальные условия

имеют четкий физический смысл. Это - начальное положение тела и его начальная скорость.

Вращательное движение тела под действием крутящего момента 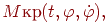где , описывается аналогично

Где

Iр - полярный момент инерции тела,

-угол поворота,

- угловая скорость,

- угловое ускорение.

При построении математических моделей систем, машин, механизмов с учетом колебаний, возникающих в них, также необходимо построить и решить дифференциальное уравнение, т.к. все виды колебаний (свободные гармонические, вынужденные) также описываются дифференциальными уравнениями.

На практике лишь небольшое число дифференциальных уравнений допускает интегрирование в квадратурах. Еще реже удается получить решение в элементарных функциях. Поэтому большое распространение при решении математических моделей с помощью ЭВМ получили численные методы решения дифференциальных уравнений.

Нахождение определенного интеграла в процессе моделирования объектов процессов или систем может применяться в следующих задачах:

1. Определение пути при переменной скорости:

1. Нахождение скорости при переменном ускорении:

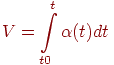
1. Определение моментов инерции тел:

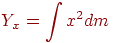
1. Нахождение работы переменной силы:

1. При решении дифференциальных уравнений.

Итак, дана функция y=f(x).

Найти интеграл этой функции на участке [a,b], т.е. найти

Если подынтегральная функция f(x) задана в аналитическом виде;

если функция f(x) непрерывна на отрезке [a,b];

если известна ее первообразная, т.е.

то интеграл может быть вычислен по формуле Ньютона-Лейбница как приращение первообразной на участке [a,b], т.е.

Но на практике формула Ньютона-Лейбница для вычисления интеграла используется редко. Численные методы интегрирования применяются в следующих случаях:

1. подынтегральная функция f(x) задана таблично на участке [a,b];
2. подынтегральная функция f(x) задана аналитически, но ее первообразная не выражается через элементарные функции;
3. подынтегральная функция f(x) задана аналитически, имеет первообразную, но ее определение слишком сложно.

В численных методах интегрирования не используется нахождение первообразной. Основу алгоритма численных методов интегрирования составляет геометрический смысл определенного интеграла. Интеграл численно равен площади S криволинейной трапеции, расположенной под подынтегральной кривой f(x) на участке [a,b] (рис.12.1).

Рис. 12.1. Геометрический смысл определенного интеграла

Суть всех численных методов интегрирования состоит в приближенном вычислении указанной площади. Поэтому все численные методы являются приближенными.

При вычислении интеграла подынтегральная функция f(x) аппроксимируется интерполяционным многочленом. На практике чтобы не иметь дело с многочленами высоких степеней, весь участок [a,b] делят на части и интерполяционные многочлены строят для каждой части деления.

Порядок вычисления интеграла численными методами следующий (рис.12.2):

1. Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.
2. В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяционным многочленом. Степень многочлена n = 0,1,2:
3. Для каждой части деления определяем площадь частичной криволинейной трапеции.
4. Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных трапеций

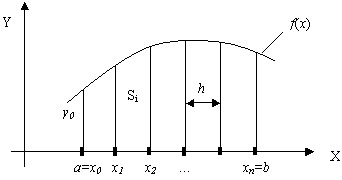
Рис. 12.2. Вычисление определенного интеграла

Нахождение приближенного значения интеграла называется квадратурой, а формулы для приближенного вычисления интеграла - квадратурными формулами или квадратурными суммами.

Разность R между точным значением интеграла и приближенным значением называется остаточным членом или погрешностью квадратурной формулы, т.е.

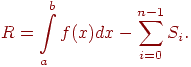
Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом нулевой степени, т.е. прямой, параллельной оси OX, то квадратурная формула называется формулой прямоугольников, а метод - методом прямоугольников.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом первой степени, т.е. прямой, соединяющей две соседние узловые точки, то квадратурная формула называется формулой трапеций, а метод - методом трапеций.

Если в каждой из частей деления интервала [a,b] подынтегральная функция аппроксимируется многочленом второй степени, то квадратурная формула называется формулой Симпсона, а метод - методом Симпсона.

 

Метод прямоугольников

Словесный алгоритм метода прямоугольников:

1. Весь участок [a,b] делим на n равных частей с шагом h=(b-a)/n.
2. Определяем значение y_i подынтегральной функции f(x) в каждой части деления, т.е.

1. В каждой части деления подынтегральную функцию f(x) аппроксимируем интерполяцион-ным многочленом степени n = 0, т.е. прямой, параллельной оси OX. В результате вся подынтегральная функция на участке [a,b] аппроксимируется ломаной линией.
2. Для каждой части деления определяем площадь S_i частичного прямоугольника.
3. Суммируем эти площади. Приближенное значение интеграла I равно сумме площадей частичных прямоугольников.

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в левых концах каждого шага, то метод называется методом левых прямоугольников (рис.12.3). Тогда квадратурная формула имеет вид

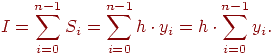
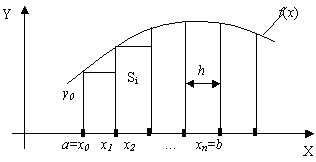
Рис. 12.3. Метод левых прямоугольников

Если высота каждого частичного прямоугольника равна значению подынтегральной функции в правых концах каждого шага, то метод называется методом правых прямоугольников (рис.12.4). Тогда квадратурная формула имеет вид

Рис. 12.4. Метод правых прямоугольников

Точность каждого метода прямоугольников имеет порядок h.

Алгоритм вычисления интеграла построим в виде итерационного процесса поиска с автоматическим выбором шага. На каждом шаге будем уменьшать шаг в два раза, то есть увеличивать число шагов n в два раза. Выход из процесса поиска организуем по точности вычисления интеграла. Начальное число шагов n=2.Схема алгоритма методов прямоугольников представлена на рис.12.5.

Рис. 12.5. Схема алгоритма метода прямоугольников (с автоматическим выбором шага)

Условные обозначения:

a,b - концы интервала,

- заданная точность,

с=0 - метод левых прямоугольников,

с=1 - метод правых прямоугольников,

S1 - значение интеграла на предыдущем шаге,

S - значение интеграла на текущем шаге.

Метод трапеций

Словесный алгоритм метода трапеций:

1. Интервал [a,b] делим на n равных частей с шагом h=(b-a)/n.
2. Вычисляем значение подынтегральной функции в каждой узловой точке

1. На каждом шаге подынтегральную функцию f(x) аппроксимируем прямой, соединяющей две соседние узловые точки. В результате вся подынтегральная функция на участке [a,b] заменяется ломаной линией проходящей через все узловые точки.
2. Вычисляем площадь каждой частичной трапеции.
3. Приближенное значение интеграла равно сумме площадей частичных трапеций, т.е.

Найдем площади S_i частичных трапеций:

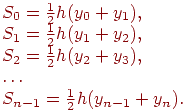
Приближенное значение интеграла равно

Точность метода трапеций имеет порядок h².

Схема алгоритма метода трапеций представлена на рис.12.6.

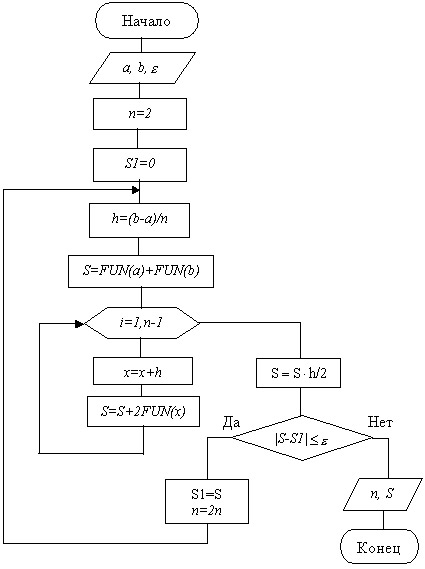
Рис. 12.6. Схема алгоритма метода трапеций (с автоматическим выбором шага)

Метод Симпсона

В методе Симпсона в каждой части деления подынтегральная функция аппроксимируется квадратичной параболой a₀x²+a₁x+a₂. В результате вся кривая подынтегральной функции на участке [a,b] заменяется кусочно-непрерывной линией, состоящей из отрезков квадратичных парабол. Приближенное значение интеграла I равно сумме площадей под квадратичными параболами.

Т.к. для построения квадратичной параболы необходимо иметь три точки, то каждая часть деления в методе Симпсона включает два шага, т.е.

L_k=2h.

В результате количество частей деления N2=n/2. Тогда n в методе Симпсона всегда четное число.

Определим площадь S₁ на участке [x₀, x₂] (рис.12.2).

Исходя из геометрического смысла определенного интеграла, площадь S₁ равна определенному интегралу от квадратичной параболы на участке [x₀, x₂]:

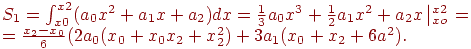
Неизвестные коэффициенты квадратичной параболы а₀, а₁, а₂ определяем из условия прохождения параболой через три узловых точки с координатами (x₀y₀), (x₁x₁), (x₂y₂).

На основании этого условия строим систему линейных уравнений:

Решая эту систему, найдем коэффициенты параболы.

В результате имеем: .

Для участка [x₂, x₄]: .

:::::::::::::::::::

Для участка [x_i-1, x_i+1]: ,

где

Суммируя все площади S₁ под квадратичными параболами, получим квадратурную формулу по методу Симпсона:

где

N2 - количество частей деления.

Точность метода Симпсона имеет порядок (h³/h⁴).

Схема алгоритма метода Симпсона представлена на рис.12.7.

Рис. 12.7. Схема алгоритма Симпсона (с автоматическим выбором шага)