В этом методе при сглаживании опытных данных аппроксимирующей кривую F(x) стремятся провести так, чтобы ее отклонения 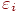 от табличных данных (уклонения) по всем узловым точкам были минимальными (рис 11.6), т.е.
от табличных данных (уклонения) по всем узловым точкам были минимальными (рис 11.6), т.е.

| (11.6) |
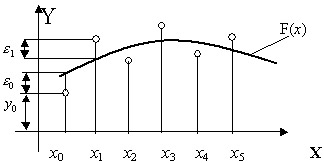
Рис. 11.6.
Избавимся от знака уклонения. Тогда условие (11.6) будет иметь вид:
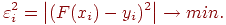
| (11.7) |
Суть метода наименьших квадратов заключается в следующем: для табличных данных, полученных в результате эксперимента, отыскать аналитическую зависимость F(x), сумма квадратов уклонений которой от табличных данных по всем узловым точкам была бы минимальной, т.е.

| (11.8) |
Для определенности задачи искомую функцию F(x) будем выбирать из класса алгебраических многочленов степени m:

| (11.9) |
Назовем многочлен (11.9) аппроксимирующим многочленом. Аппроксимирующий многочлен не проходит через все узловые точки таблицы. Поэтому его степень m не зависит от числа узловых точек. При этом всегда m < n. Степень m может меняться в пределах 
Если m=1, то мы аппроксимируем табличную функцию прямой линией. Такая задача называется линейной регрессией.
Если m=2, то мы аппроксимируем табличную функцию квадратичной параболой. Такая задача называется квадратичной аппроксимацией.
Если m=3, то мы аппроксимируем табличную функцию кубической параболой. Такая задача называется кубической аппроксимацией.
Уточним метод наименьших квадратов: для табличной функции, полученной в результате эксперимента, построить аппроксимирующий многочлен (11.9) степени m, для которого сумма квадратов уклонений по всем узловым точкам минимальна, т.е.

| (11.10) |
Изменим вид многочлена Pm. Поставим на последнее место слагаемые, содержащие xm. На предпоследнее - слагаемые, содержащие xm-1 и т.д. В результате получим:

| (11.11) |
или

При этом изменим индексы коэффициентов многочлена. Тогда условие (11.8) будет иметь вид:

где
xi и yi- координаты узловых точек таблицы,
aj, 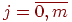 -неизвестные коэффициенты многочлена (11.11).
-неизвестные коэффициенты многочлена (11.11).
Необходимым условием существования минимума функции S является равенство нулю ее частных производных по каждой aj.

В результате получили систему линейных уравнений. Раскрывая скобки и перенося свободные члены в правой части уравнений, получим в нормальной форме систему линейных уравнений:

| (11.12) |
где
aj- неизвестные системы линейных уравнений (11.12),
 - коэффициенты системы линейных уравнений (11.12),
- коэффициенты системы линейных уравнений (11.12),
 - свободные члены системы линейных уравнений (11.12),
- свободные члены системы линейных уравнений (11.12),
Порядок системы равен m+1.
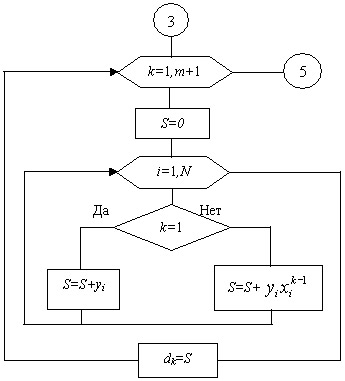
При ручном счете коэффициенты ck и свободные члены dj удобно определять, пользуясь таблицей 11.2:
Таблица 11.2.







 - неизвестные системы линейных уравнений (11.13),
- неизвестные системы линейных уравнений (11.13),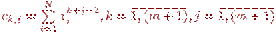 - коэффициенты системы линейных уравнений (11.13),
- коэффициенты системы линейных уравнений (11.13), - свободные члены системы линейных уравнений (11.13),
- свободные члены системы линейных уравнений (11.13), ,
,
 .
. 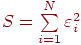 .
. 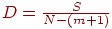 .
.