Общий вид дифференциального уравнения
| (12.1) |
Нормальная форма дифференциального уравнения
| (12.2) |
где
y=y(x) -неизвестная функция, подлежащая определению,
f(x,y) - правая часть дифференциального уравнения в нормальной форме, равная первой производной функции y(x). В функцию f(x,y) помимо аргумента x входит и сама неизвестная функция y(x).
Пример:
- общий вид дифференциального уравнения первого порядка,
- нормальная форма этого же уравнения.
Если неизвестная функция у зависит от одного аргумента x, то дифференциальное уравнение вида
называется обыкновенным дифференциальным уравнением.
Если функция у зависит от нескольких аргументов, то такое дифференциальное уравнение называется дифференциальным уравнением в частных производных.
Общим решением обыкновенного дифференциального уравнения
является семейство функций у=у(х,с) (рис 12.8):
Рис. 12.8.
При решении прикладных задач ищут частные решения дифференциальных уравнений. Выделение частного решения из семейства общих решений осуществляется с помощью задания начальных условий:
| (12.3) |
т.е. начальной точки с координатами (х0, у0).
Нахождение частного решения дифференциального уравнения
|
| (12.2) |
удовлетворяющего начальному условию
|
| (12.3) |
называется задачей Коши.
В численных методах задача Коши ставится следующим образом: найти табличную функцию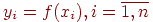 
которая удовлетворяет заданному дифференциальному уравнению (12.2) и начальному условию (12.3) на отрезке [a,b] с шагом h, то есть найти таблицу
| i | x | y |
| 0 | x0 | y0 |
| 1 | x1 | y1 |
| 2 | x2 | y2 |
| 3 | x3 | y3 |
| ... | ... | ... |
| n | xn | yn |
Здесь
h - шаг интегрирования дифференциального уравнения,
a=x0 - начало участка интегрирования уравнения,
b=xn - конец участка,
n=(b-a)/h - число шагов интегрирования уравнения.
На графике (рис 12.9) решение задачи Коши численными методами представляется в виде совокупности узловых точек с координатами (xi,yi), 
.
Рис. 12.9.
Методы Рунге - Кутта
Наиболее эффективными и часто встречаемыми методами решениями задачи Коши являются методы Рунге - Кутта. Они основаны на аппроксимации искомой функции у(х) в пределах каждого шага многочленом, который получен при помощи разложения функции у(х) в окрестности шага h каждой i-ой точки в ряд Тейлора:
| (12.5) |
Усекая ряд Тейлора в различных точках и отбрасывая правые члены ряда, Рунге и Кутт получали различные методы для определения значений функции у(х) в каждой узловой точке. Точность каждого метода определяется отброшенными членами ряда.
Метод Рунге - Кутта 1-го порядка (метод Эйлера)
Отбросим в (12.4) члены ряда, содержащие h2, h3, h4:.
Тогда 
Так как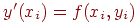 
Получим формулу Эйлера:
| (12.5) |
Так как точность методов Рунге-Кутта определяется отброшенными членами ряда (12.4), то точность метода Эйлера на каждом шаге составляет 
.
Алгоритм метода Эйлера можно построить в виде двух программных модулей: основной программы и подпрограммы ELER, реализующей метод.
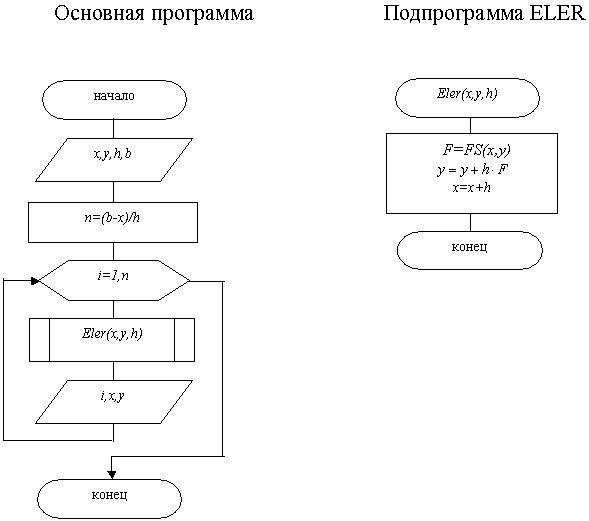
Рис. 12.10. Схема алгоритма метода Эйлера
Здесь
(x,y)-при вводе начальная точка, далее текущие значения табличной функции,
h-шаг интегрирования дифференциального уравнения,
b-конец интервала интегрирования.
Рассмотрим геометрический смысл метода Эйлера.
Формула Эйлера имеет вид:
где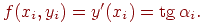 
Тогда формула Эйлера принимает вид:
где
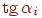- тангенс угла наклона касательной к искомой функции у(x) в начальной точке каждого шага.
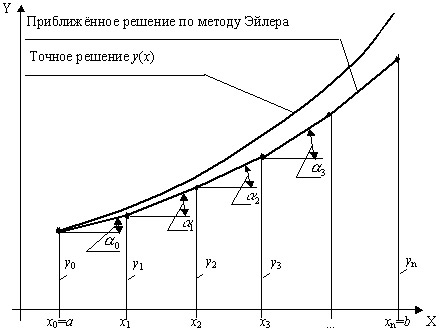
Рис. 12.11. Геометрический смысл метода Эйлера
В результате в методе Эйлера на графике (рис 12.10) вся искомая функция y(x) на участке [a,b] аппроксимируется ломаной линией, каждый отрезок которой на шаге h линейно аппроксимирует искомую функцию. Поэтому метод Эйлера получил еще название метода ломаных.
В методе Эйлера наклон касательной в пределах каждого шага считается постоянным и равным значению производной в начальной точке шага xi. В действительности производная, а, значит, и тангенс угла наклона касательной к кривой y(x) в пределах каждого шага меняется. Поэтому в точке xi+h наклон касательной не должен быть равен наклону в точке xi. Следовательно, на каждом шаге вносится погрешность.
Первый отрезок ломаной действительно касается искомой интегральной кривой y(x) в точке (x0,y0). На последовательных же шагах касательные проводятся из точек (xi,yi), подсчитанных с погрешностью. В результате с каждым шагом ошибки накапливаются.
Основной недостаток метода Эйлера - систематическое накопление ошибок. Поэтому метод Эйлера рекомендуется применять для решения дифференциальных уравнений при малых значениях шага интегрирования h.
Метод Рунге - Кутта 2-го порядка (модифицированный метод Эйлера)
Отбросим в (12.4) члены ряда, содержащие h3, h4, h5:.
Тогда
| (12.6) |
Чтобы сохранить член ряда, содержащий h2, надо определить вторую производную y"(xi).Ее можно аппроксимировать разделенной разностью 2-го порядка
Подставляя это выражение в (12.6), получим
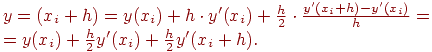
Окончательно, модифицированная или уточненная формула Эйлера имеет вид:
| (12.7) |
Как видно, для определения функции y(x) в точке i+1 необходимо знать значение правой части дифференциального уравнения f(xi+1, yi+1) в этой точке, для определения которой необходимо знать предварительное значение yi+1.
Для определения предварительного значения yi+1 воспользуемся формулой Эйлера. Тогда все вычисления на каждом шаге по модифицированной или уточненной формуле Эйлера будем выполнять в два этапа:
На первом этапе вычисляем предварительное значение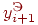 
по формуле Эйлера
На втором этапе уточняем значение y=i+1 по модифицированной или уточненной формуле Эйлера
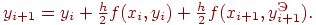
Точность метода определяется отброшенными членами ряда Тейлора (12.4), т.е. точность уточненного или модифицированного метода Эйлера на каждом шаге 
.
Рассмотрим геометрический смысл модифицированного метода Эйлера.
Так как
то модифицированную формулу Эйлера можно представить в виде:
где
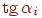- тангенс угла наклона касательной к искомой функции у(х) в начальной точке каждого шага,
- тангенс угла наклона касательной к искомой функции у(х) в конечной точке каждого шага.
Рис. 12.12. Геометрический смысл модифицированного метода Эйлера
Здесь
P1 - накопленная ошибка в (i+1)й точке по методу Эйлера,
P2 - накопленная ошибка в (i+1)й точке по модифицированному методу Эйлера.
Как видно из рис.12.11, в первой половине каждого шага, то есть на участке [xi, xi+h/2], искомая функция y(x) аппроксимируется прямой, которая выходит из точки (xi, yi) под углом, тангенс которого 
Во второй половине этого же шага, т.е. на участке [xi + h/2,xi + h], искомая функция y(x) аппроксимируется прямой, которая выходит из точки с координатами
под углом, тангенс которого
В результате в модифицированном методе Эйлера функция у(х) на каждом шаге аппроксимируется не одной прямой, а двумя.
Алгоритм модифицированного метода Эйлера можно построить в виде двух программных модулей: основной программы и подпрограммы МELER, реализующей метод (рис. 12.13).
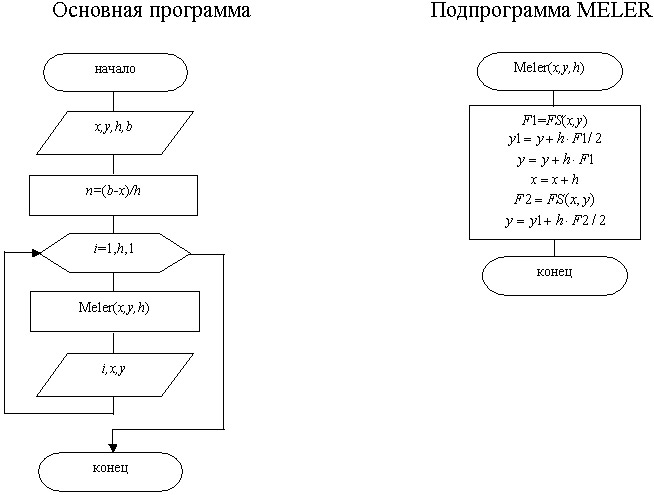
Рис. 12.13. Схема алгоритма модифицированного метода Эйлера
Здесь
(x,y)-при вводе начальная точка, далее текущие значения табличной функции,
h-шаг интегрирования дифференциального уравнения,
b-конец интервала интегрирования.
