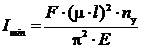Шкив с диаметром D 1 и с углом наклона ветвей ремня к горизонту α1 делает n оборотов в минуту и передает мощность P кВт. Два других шкива имеют одинаковый диаметр D 2, одинаковые углы наклона ветвей ремня к горизонту α2 и каждый из них передает мощность P /2 (рисунок 33). Необходимо подобрать диаметр вала d при [σ] = 100 МПа.
Таблица 11
Данные к задаче 10
| Номер | Номер | P | n | а | в | с | D 1 | D 2 | α1 | α2 |
| строки | схемы | кВт | об/мин | м | м | м | м | м | град | град |
| 1 | 1 | 10 | 100 | 1,1 | 1,1 | 1,1 | 1,1 | 1,1 | 10 | 10 |
| 2 | 2 | 20 | 200 | 1,2 | 1,2 | 1,2 | 1,2 | 1,2 | 20 | 20 |
| 3 | 3 | 30 | 300 | 1,3 | 1,3 | 1,3 | 1,3 | 1,3 | 30 | 30 |
| 4 | 4 | 40 | 400 | 1,4 | 1,4 | 1,4 | 1,4 | 1,4 | 40 | 40 |
| 5 | 5 | 50 | 500 | 1,5 | 1,5 | 1,5 | 1,5 | 1,5 | 50 | 50 |
| 6 | 6 | 60 | 600 | 1,6 | 1,6 | 1,6 | 1,6 | 1,6 | 60 | 60 |
| 7 | 7 | 70 | 700 | 1,7 | 1,7 | 1,7 | 1,7 | 1,7 | 70 | 70 |
| 8 | 8 | 80 | 800 | 1,8 | 1,8 | 1,8 | 1,8 | 1,8 | 80 | 80 |
| 9 | 9 | 90 | 900 | 1,9 | 1,9 | 1,9 | 1,9 | 1,9 | 90 | 90 |
| 10 | 100 | 1000 | 2 | 2 | 2 | 2 | 2 | 0 | 0 | |
| Е | Д | В | Г | Д | Б | А | Е | Д | Е |
Рисунок 33 − Схемы к задаче 10
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
Основные понятия
Под действием сжимающей силы стержень может утратить первоначальную форму равновесия и искривиться. Произойдет потеря устойчивости стержня. Наименьшая сила, при которой происходит потеря устойчивости, называется критической и определяется по формуле Эйлера:
где F кр – критическая сила;
Е – модуль упругости материала стержня;
I min – минимальный осевой момент инерции сечения стержня;
μ – коэффициент приведения длины, зависящий от способа закрепления концов стержня (рисунок 64);
l – длина стержня;
μ ∙ l = l пр – приведенная длина стержня.
Рисунок 34 − Значения коэффициента μ приведенной длины и критической
силы F кр для сжатых стержней при различных способах закрепления концов
Напряжения, вызванные критической силой, называются критическими и определяются по формуле Эйлера:
,
где λ – гибкость стержня, 
;
– минимальный радиус инерции сечения;
А – площадь поперечного сечения стержня.
Формула Эйлера применима при условии, что критическое напряжение не превышает предела пропорциональности материала σкр. Обычно это условие выражают через гибкость стержня и записывают в виде
где λпр – предельное значение гибкости, которое определяет границу применимости формулы Эйлера.
Формулой Эйлера можно пользоваться, если гибкость стержня λ ≥ λпр,
если λ < λпр, то пользоваться формулой Эйлера нельзя.
При значениях гибкости от 0 до 40 
50 стержень настолько короткий, что практически разрушается при потере прочности, поэтому критическое напряжение равно пределу текучести: 
.
При значениях гибкости, лежащих в интервале 50 ≤ λ 
λ пр, стержень теряет устойчивость, деформируясь в упруго-пластической области, поэтому критическое напряжение σкр определяют по эмпирической формуле Ф. С. Ясинского:
σкр = а – b λ + cλ2, F кр = σкр A,
где а, b, с – коэффициенты, зависящие от материала и имеющие размерность напряжения. Они приведены в таблице 12.
Таблица 12
Опытные коэффициенты для определения σкр, МПа
| Материал | а | b | с |
| Сталь Ст3 Сталь Ст5 Чугун Сосна (сжатие вдоль волокон) | 310 464 776 29,3 | 1,14 3,62 12 0,194 | 0 0 0,053 0 |
Критическая сила является недопустимой для сжатых стержней.
Определение допускаемой сжимающей силы [ F ] производят двумя способами. Первый способ используется, когда для рассчитываемого стержня известны длина, способ закрепления концов, форма и размеры поперечного сечения, материал, коэффициент запаса на устойчивость. Вначале определяют критическую силу F кр = sкр ∙ А, а затем допускаемую силу [ F ]: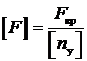 
,
де [ n у] – допускаемый коэффициент запаса на устойчивость.
Значения допускаемых коэффициентов запаса на устойчивость [ n у] для различных материалов приведены в таблице 13.
Таблица 13
Допускаемые коэффициенты запаса на устойчивость для различных материалов
| Материал | [ n y] |
| Сталь Ст 3 | 1,8 3
|
| Сталь Ст 5 | 1,8 3
|
| Чугун | 5 5,5
|
| Сосна (сжатие вдоль волокон) | 2,8 3,2
|
Второй способ основан на применении таблиц j (l). Сначала определяют гибкость стержня λ, затем по таблице находят j (l) и вычисляют [ F ] по формуле: [ F ] = j (l). [sс] . А,
где j(l)– коэффициент уменьшения допускаемого напряжения при сжатии [sс].
Значения коэффициента j в зависимости от гибкости λ и материала стержня приведены в таблице 14.
Для расчета критического напряжения, критической силы, допускаемой сжимающей силы и коэффициента запаса на устойчивость можно использовать блок-схему, представленную на рисунке 35.
Таблица 14
Значение коэффициента продольного изгиба j (l)
для различных материалов
| Гибкость λ | Значение j (l) | |||
| Сталь Ст3, Ст4 | Сталь Ст5 | Чугун | Дерево | |
| 0 | 1,00 | 1,00 | 1,00 | 1,00 |
| 10 | 0,99 | 0,98 | 0,97 | 0,99 |
| 20 | 0,97 | 0,96 | 0,91 | 0,97 |
| 30 | 0,95 | 0,93 | 0,81 | 0,93 |
| 40 | 0,92 | 0,89 | 0,69 | 0,87 |
| 50 | 0,89 | 0,85 | 0,57 | 0,80 |
| 60 | 0,86 | 0,80 | 0,44 | 0,71 |
| 70 | 0,81 | 0,74 | 0,34 | 0,60 |
| 80 | 0,75 | 0,67 | 0,26 | 0,48 |
| 90 | 0,69 | 0,59 | 0,20 | 0,38 |
| 100 | 0,60 | 0,50 | 0,16 | 0,31 |
| 110 | 0,52 | 0,43 | – | 0,25 |
| 120 | 0,45 | 0,37 | – | 0,22 |
| 130 | 0,40 | 0,32 | – | 0,18 |
| 140 | 0,36 | 0,28 | – | 0,16 |
| 150 | 0,32 | 0,25 | – | 0,14 |
| 160 | 0,29 | 0,23 | – | 0,12 |
| 170 | 0,26 | 0,21 | – | 0,11 |
| 180 | 0,23 | 0,19 | – | 0,10 |
| 190 | 0,21 | 0,17 | – | 0,09 |
| 200 | 0,19 | 0,15 | – | 0,08 |
| 210 | 0,17 | 0,14 | – | – |
| 220 | 0,16 | 0,13 | – | – |
Рисунок 35 − Блок-схема вычисления σкр, F кр, [ F ] и n у
Практически расчет на устойчивость ведется с использованием коэффициента j – коэффициента уменьшения допускаемого напряжения при сжатии [sс].
Условие устойчивости имеет вид
Расчет на устойчивость сводится к недопущению потери устойчивости, т.е. искривления стержня.
Подбор поперечного сечения стержня при заданных длине, сжимающей силе и материале выполняется с использованием таблиц значений j (l) методом последовательных приближений в следующем порядке.
1. Задают произвольное значение j. Например, полагают j = 0,5.
2. Вычисляют допускаемое напряжение на устойчивость:
[sу] = j ∙ [sс].
3. Определяют площадь поперечного сечения из условия
устойчивости:
A бр³ F / (j ∙ [sс]).
4. Подбирают размеры сечения или номер профиля. Вычисляют
площадь А, минимальный момент инерции I min, минимальный радиус инерции i minпоперечного сечения.
5. Определяют гибкость стержня l.
6. Если гибкость стержня l > 220, то считают, что заданная сила
F равна допускаемой [ F ]: 
,
где F кр – критическая сила (определяется по формуле Эйлера), а n у – коэффициент запаса на устойчивость (выбирается по таблице 13).
Тогда можно определить значение наименьшего момента инерции I min по формуле
.
7. Если гибкость стержня l 
220, то для полученной гибкости
находят истинное значение jи.
8. Вычисляют действующее напряжение s = 
.
9. Вычисляют допускаемое напряжение [sу] = jи ∙[sс].
10. Сравнивают действующее напряжение с допускаемым, вычисляя относительную разницу k:
.
11. Если k > 0, то имеем недонапряжение, если k < 0, то имеем
перенапряжение.
12. Сечение считают подобранным, если s и [sу] отличаются не
более, чем на 5%, т.е. |k| £ 5%.
13. Если |k| > 5%, то в качестве второго приближения берут
j2 = j + jи и повторяют расчет, пока не будет выполняться условие |k| £ 5%.
Подбор сечения по изложенному алгоритму представлен в виде
блок-схемы (рисунок 36).
В сопротивлении стержней продольному изгибу основную роль играет
гибкость стержня и, следовательно, величина наименьшего радиуса инерции сечения, поэтому существенным является вопрос не только величины площади сечения, как при расчете на прочность, но и формы поперечного сечения.
Для наиболее оптимального выбора сечения необходимо конструировать
сечение так, чтобы при определенной площади величина наименьшего радиуса инерции была бы возможно большей. Для этого прежде всего следует стремиться к тому, чтобы центральные моменты инерции сечения были равны. Такой стержень будет оказывать одинаковое сопротивление потере устойчивости в любом направлении.
Далее, необходимо стремиться к получению при данной площади
наибольших центральных моментов инерции. Для этого надо разместить материал сечения по возможности дальше от центра тяжести. Этим условиям хорошо удовлетворяют трубчатое сечение или сечение, составленное из двух швеллеров, раздвинутых на определенное расстояние.
На выбор материала для сжатых стержней влияют два фактора:
1. Если sкр < sпц (при большой гибкости), то единственной
механической характеристикой, влияющей на устойчивость, является модуль продольной упругости Е, а Е мало зависит от марки стали. Поэтому для тонких и длинных стержней применяют низколегированные стали.
2. Для стержней средней и особенно малой гибкости sкр
существенно зависит от предела текучести или предела прочности материала. Применение высоколегированных сталей для этих стержней дает существенную экономию материала.
Значение проверки на устойчивость велико. Достаточно сказать,
что все значительные катастрофы инженерных сооружений произошли вследствие потери устойчивости сжатых элементов конструкции. Особая опасность потери устойчивости заключается в том, что обычно она наступает внезапно.
|
Рисунок 36 − Блок-схема подбора сечения из расчета на устойчивость
Пример 11
Определить величину F кр и sкр для дюралюминиевого стержня кольцевого сечения: 
, 
, 
, 
, 
(рисунок 37).
Рисунок 37 − Определение критической силы для стержня
кольцевого сечения
Осевой момент инерции кольцевого сечения стержня:
.
Площадь поперечного сечения стержня:
.
Радиус инерции поперечного сечения: 
При заданном способе закрепления концов стержня 
Гибкость стержня: 
Критерий применимости формулы Эйлера:
Так как λ > λпр, то F кр можно определить по формуле Эйлера:
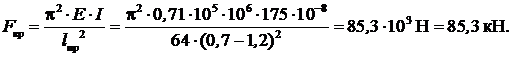
Критическое напряжение:
Пример 12
Колонна, составленная из двух швеллеров (рисунок 38), нагружена силой
F = 200 кН, l = 2,5 м.
Рисунок 38 − Подбор поперечного сечения колонны з расчета на устойчивость
Подобрать номер швеллера, если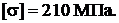 
Сначала нужно выявить главную центральную ось заданного сечения из двух швеллеров с минимальным значением момента инерции. В нашем примере такой осью будет ось симметрии o y (рисунок 38).
Момент инерции произвольного сечения относительно оси o y, параллельной главной оси сечения o y 1 и удаленной от нее на расстояние a, можно вычислить по формуле
,
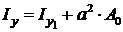где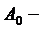 
площадь сечения.
Так как наша колонна состоит из двух одинаковых швеллеров, состыкованных вплотную друг к другу, то
,
где А 0 – площадь одного швеллера.
Площадь всего сечения А = А 0.
Подбор размеров сечения ведется путем последовательного приближения. Обычно задают значение φ и определяют A. Для первого приближения примем произвольно 
Тогда из условия устойчивости
По сортаменту (ГОСТ 8240 – 72) исследуем швеллер № 10:
, 
, 
, 
.
Для рассматриваемого сечения, состоящего из двух швеллеров
№ 10, имеем:
Гибкость колонны 
Для стержня с защемленным концом 
По таблице для стали марки Ст3, интерполируя, находим истинное значение 
для выбранного профиля 
Действующее напряжение: 
допустимое напряжение 
Перенапряжение составляет 28,4%.
Второе приближение.
Задаемся 
тогда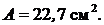 
Исследуем швеллер № 12, 
Для сечения 
Гибкость колонны 
Коэффициент 
Напряжение в колонне:
Недонапряжение составляет 15,1%.
Анализируя расчеты, заметим, что сечение из двух швеллеров № 10 дает большое перенапряжение, а из двух швеллеров № 12 – существенное недонапряжение. Уменьшить это недонапряжение мы не можем, так как ближайший стандартный профиль с меньшим поперечными размерами – это уже рассмотренный нами швеллер № 10.
Поскольку размеры сечений прокатных профилей от номера к номеру изменяются скачкообразно, во многих случаях не удается подобрать такое сечение, чтобы расхождение в напряжениях не превышало 5 %.
Итак, принимаем сечение из двух швеллеров № 12.
Задача 11
Устойчивость сжатых стержней.
