Метод сравнения перемещений (деформаций) наиболее простой. Суть этого метода заключается в том, что дополнительные уравнения составляются из условий равенства нулю прогибов на опорах балки. Рассмотрим этот метод на примере.
Пример 6
Для балки, изображённой на рисунке 25, требуется определить опорные реакции и построить эпюры поперечных сил Qy и изгибающих моментов М Z
Рисунок 25 − Расчетная схема статически неопределимой балки
Балка имеет 4 опорные связи и является один раз статически неопределимой. Для определения неизвестных реакций МА, R А, H А и RB имеем только три уравнения равновесия статики:
1. ∑ Х = 0; (11)
откуда следует, что H А = 0.
2. ∑ Y = 0; (12)
R А − q ∙3+ RB − F = 0;
R А + RB = 380.
3. ∑ М B = 0; (13)
МА + 6∙ R А − q ∙3∙4,5 + M + F ∙2 = 0;
МА + 6∙ R А = 1310.
Дополнительное четвертое уравнение составим, исходя из условия, что на опоре В прогиб yB равен нулю. Прогиб в опоре определим, используя универсальное уравнение упругой линии (метод начальных параметров), которое применительно к данной задаче имеет вид:
4. EI yB = 0; (14)
EI yB = EI y 0 + EI φ0 ∙ x + МА ∙62 /2 + R А ∙63 /6 − q ∙64 /24 + q ∙34 /24 + М ∙12 /2 = 0.
Так как качало координат помещено в защемлении, начальные параметры y 0 = 0 и φ0 = 0, где y 0 − прогиб балки при х = 0, φ0 − угол поворота сечения балки при х = 0.
С учетом этого уравнение (14) имеет вид
МА + 2∙ R А = 330.
Решая совместно уравнения (3) и (4), получим:
,
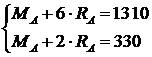- откуда R А = 245 кН, МА = − 160 кHм.
Затем, подставив в уравнение (12) найденное значение реакции R А, определим реакцию RB = 380 – 245 = 135 кН.
Для проверки правильности вычисленных реакций составим уравнение
моментов всех сил относительно опоры А:
∑ m А = −120∙3∙1,5 + 270 −135∙6 + 20∙8 = 0
Равенство нулю суммы моментов означает, что реакции определены
правильно. Определив значения реакций МА, R А, и RB, можно приступить к
построению эпюр внутренних усилий.
На рисунке 26 приведены: схема балки, эпюры поперечных сил
Qy, кН и изгибающих моментов М Z, кНм.
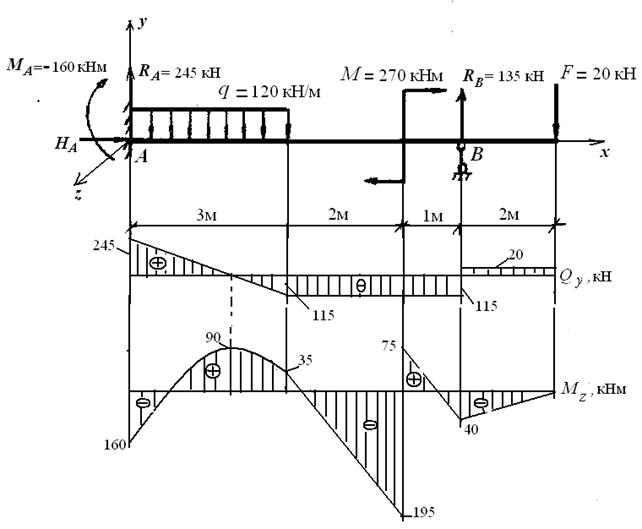
Рисунок 26 − Расчет статически неопределимой балки.
Эпюры поперечных сил Qy и изгибающих моментов М Z
Рассмотрим ещё один пример расчета статически неопределимой балки.
Пример 7
Определить размеры h, b прямоугольного поперечного сечения стальной балки (рисунок 27), если [σи] = 160 МПа, E = 2·105 МПа и h/b = 2. Определить прогибы посредине пролета балки и на конце консоли. Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:
;
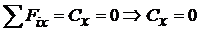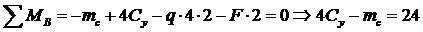. (15)
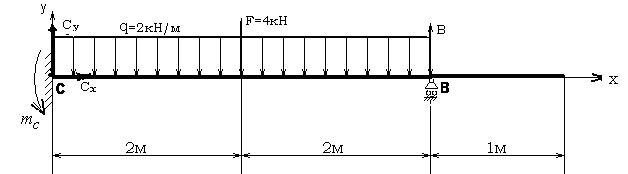
Рисунок 27 − Расчетная схема статически неопределимой балки
Число неизвестных реакций 4, уравнений статики 3: балка один раз статически неопределима. Целесообразные уравнения статики:
;
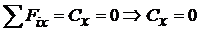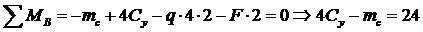. (15)
Дополнительное уравнение составим, исходя из условия, что на опоре B прогиб равен нулю:
. Так как начало координат помещено в защемлении, начальные параметры y 0 = 0 и φ0 = 0. Тогда из уравнения прогибов получим:
(16)
Из уравнений (15) и (16) следует: Су = 7,75 кН, mc = 7 кН∙м.
Определим опорную реакцию B:
,
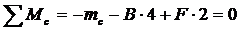откуда В = 4,25 кН.
Рисунок 28 − Пример 9. Эпюры поперечных сил Q,
изгибающих моментов M и прогибов y
Проверка вычислений реакций:
.
Эпюры 
и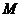 
показаны на рисунке 51, б, в.
Размеры сечения балки определим из условия прочности по нормальным напряжениям:
; 
;
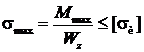Момент инерции сечения
Жесткость сечения
Прогиб посередине пролета балки 
;
.
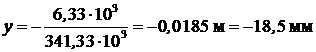Прогиб на конце консоли (х = 5 м):
откуда 
Изогнутая ось балки показана на рисунке 51, г. Необходимо отметить,
что консольная часть балки не деформируется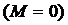 
, но перемещается за счет деформации пролетной части. Точка D – точка перегиба упругой линии.
Задача 8
