Рассмотрим статически определимую систему, где для определения внутренних сил в элементах достаточно уравнений статики.
Порядок решения статически определимых стержней.
1. Разбить стержень на участки. Участок от участка отделяется либо
сечением, где приложена сосредоточенная внешняя нагрузка F, либо сечением, где изменяется площадь поперечного сечения стержня. Участки нумеруем, начиная от свободного конца стержня (конца, где нет заделки).
Обозначим:
i – номер участка, i = 1, 2,….. п,
п – число участков.
2. Определить внутренние продольные силы Ni на каждом i –том участке. Эти силы начинаем определять от свободного конца стержня, используя метод сечений. Величина продольной силы равна алгебраической сумме всех внешних сил, действующих на стержень по одну сторону от рассматриваемого сечения.
Продольная сила N считается положительной, если она направлена от рассматриваемого сечения, и отрицательной, когда направлена к этому сечению. Условимся, что вектор N направлен от рассматриваемого сечения. Тогда получаемый в результате подсчета знак укажет на характер деформации: плюс – растяжение, минус – сжатие.
3. По найденным значениям Ni построить эпюру внутренних сил N.
На эпюре N в сечении, где приложена сосредоточенная внешняя нагрузка F,
будет скачок на величину этой силы.
4. Построить эпюру нормальных напряжений σх. Продольная сила N связана с нормальными напряжениями σ, которые распределяются по сечению равномерно:
.
5. Построить эпюру относительных продольных деформаций εx:
εx = σ x / E
6. Построить эпюру перемещений δ:
δ =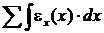 
.
Эпюру перемещений δ строим от заделки, где перемещение δ = 0, так
как заделка считается абсолютно жесткой. Перемещение δ в произвольном сечении стержня равно сумме деформаций ∆ li участков, расположенных между сечением и заделкой.
Абсолютные деформации стержня ∆ l определим по формуле:
,
,
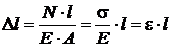где l – длина стержня, м; li – длина i –го участка стержня, м;
E – модуль продольной упругости материала (модуль Юнга), Па;
E ∙ A – жесткость стержня при растяжении и сжатии, кН.
7. Проверить условие прочности:
σmax =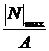 
≤ [σ],
где N – продольная сила, Н;
A – площадь поперечного сечения, м2;
[σ] – допускаемое напряжение материала при растяжении или сжатии, Па.
При построении эпюр продольных сил N, нормальных напряжений σх , относительных продольных деформаций εx, перемещений δ следует положительные значения указанных величин откладывать вправо от вертикальной базисной линии или вверх от горизонтальной базисной линии; отрицательные значения N, σх , εx, δ следует откладывать в противоположном направлении, т.е. либо влево, либо вниз.
Пример 1
Определить площадь поперечных сечений на всех участках чугунного стержня (рисунок 2, а). Построить эпюры продольных сил N, напряжений σ, относительных продольных деформаций ε х и перемещений δ. Принять для чугуна [σс] = 180 МПа, [σр] = 60 МПа, Е = 105 МПа = 1011 Па.
Рисунок 2 − Построение внутренних продольных сил N, сил, напряжений σ, относительных продольных деформаций ε х и перемещений δ.
Рассматриваемый стержень имеет одну опорную реакцию R, и для него можно составить лишь одно уравнение статики: Σ Х = 0. Значит, эта система статически определима: Σ Х = R – F 1+ F 2 – F 3 = 0, откуда R = 1300 кН.
Стержень подвергается растяжению – сжатию. Выделяем участки нагружения 1 – 4 (между точками приложения внешних сил), в пределах которых намечаются сечения I – IV. Участки нумеруем от свободного конца стержня.
Для определения N 1 на первом участке рассмотрим равновесие части стержня, расположенной выше сечения I – I, а часть стержня, наиболее нагруженную и содержащую заделку, отбросим (рисунок 3).
Рисунок 3 − Определение внутренних сил N 1
Уравнение статики Σ Х = 0 имеет вид
Σ Х = N 1 = 0, N 1= 0.
Так как на первом участке продольная сила N 1 равна нулю (N 1= 0), первый участок не деформируется.
Аналогично определяются продольные силы N 2 , N 3 , N 4 (рисунок 4).
Рисунок 4 − Определение внутренних сил Ni
На часть стержня, расположенную выше сечения II — II, действуют сила F 1 = 400 кН и продольная сила N 2 . Уравнение статики имеет вид:
Σ Х = 0, N 2 + F 1 = 0, F 1 = – 400 кН.
Полученный в результате подсчета знак минус при N 2 указывает, что N 2 имеет направление, противоположное заданному, и что второй участок сжат.
Для третьего участка (рисунок 2) уравнение статики запишется так:
Σ Х = 0,
F 1– F 2 + N 3 = 0,
N 3 = – F 1 + F 2 = – 400 + 700 = 300кН.
Третий участок растянут, т. к. продольная сила N 3 направлена от сечения.
Для четвертого участка (рисунок 2) уравнение статики имеет вид:
Σ Х = 0,
F 1– F 2 + F 3 + N 4 = 0,
N 4 = – F 1 + F 2 – F 3 = – 400 + 700 – 1600 = – 1300кН.
Направление силы N 4 противоположно заданному, четвертый участок сжат.
По вычисленным значениям Ni строим эпюру продольных сил (рисунок 2, б).
Из условия прочности 
определяем площади поперечных сечений на участках стержня:
на первом и на втором участках
,
,
на третьем участке
на четвертом участке
.
Рассчитываемый стержень с найденными площадями поперечных сечений показан на рисунке 2, в.
Нормальные напряжения:
на первом участке
,
на втором участке
,
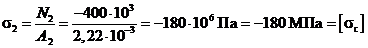на третьем участке
,
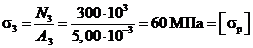на четвертом участке
.
Проделанные расчеты напряжений являются проверочными. На рисунке 2, г показана эпюра нормальных напряжений.
Вычислим относительные продольные деформации ε х i по формуле
для всех участков стержня:
на первом участке
ε х 1 
,
на втором участке
ε х 2 = 
,
на третьем участке
ε х 3 = 
,
на четвертом участке
ε х 4 = 
.
На рисунке 2, д показана эпюра относительных продольных деформаций ε х i.
Абсолютные деформации стержня ∆ l i определим по формуле:
∆ l i = ε х i ∙ li
для всех участков стержня:
на первом участке ∆ l 1 = ε х 1 ∙ l 1 = 0 ∙ l 1 = 0,
на втором участке ∆ l 2 = ε х 2 ∙ l 2 = 
∙ 0,40∙103 = – 0,72мм,
на третьем участке ∆ l 3 = ε х 3 ∙ l 3 = 
∙ 1,00∙103 = 0,60 мм,
на четвертом участке ∆ l 4 = ε х 4 ∙ l 4 = ∙ 0,25∙103 = – 0,45мм.
Определим перемещения δ на границах участков, используя тот факт, что перемещение δ является интегральной функцией по отношению к относительной продольной деформации ε х. Эпюру перемещение δ начинаем строить от заделки. В заделке перемещение δзадел = 0. Перемещение любого сечения стержня равно сумме деформаций участков, расположенных между сечением и опорой (заделкой), т.е. сумме площадей эпюры ε х, расположенных между рассматриваемым сечением и заделкой.
Перемещение точки В обусловлено деформацией участка IV:
δB = ∆ l 4 = – 0,45мм,
Перемещение точки С складывается из деформаций участков IV и III:
δc = ∆ l 4+∆ l 3= – 0,45 + 0,60 = 0,15 мм,
Перемещение точки D складывается из деформаций участков IV, III и II: δD = ∆ l 4+∆ l 3 +∆ l 2= – 0,45 + 0,60 – 0,72 = – 0,57 мм,
Перемещение точки K складывается из деформаций участков IV, III, II и I: δK = ∆ l 4+∆ l 3 +∆ l 2 + ∆ l 1 = – 0,45 + 0,60 – 0,72 + 0 = – 0,57 мм.
Точка K опускается по вертикали вниз на 0, 57 мм.
По вычисленным значениям δ строится эпюра перемещений (рисунок 2, е).
Задача 1. Растяжение и сжатие
(статически определимая система)
Произвести расчет ступенчатого стержня (рисунок 5) на прочность и жесткость. Стержень находится под действием сил F. Материал стержня – сталь с допускаемым напряжением [σ], равным 210 МПа и модулем продольной упругости Е, равным 200 ГПа = 2∙105 МПа, А – площадь поперечного сечения. Данные к задаче приведены в таблице 1. Собственный вес стержня не учитывать. Необходимо:
1) вычислить продольные силы N на участках стержня и построить эпюру N;
2) вычислить нормальные напряжения σ на участках стержня и построить эпюру σ по длине стержня;
3) вычислить относительные продольные деформации ε участков стержня и построить эпюру ε;
4) вычислить абсолютные продольные деформации стержня ∆ li участков стержня и построить эпюру перемещений δ;
5) проверить условие прочности: σmax = 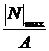≤ [σ].
Таблица 1
Данные к задаче 1
| Номер строки | Схема по рис. 5. | А, см 2 | F 1, кH | F 2, кH | a, м | b, м | с, м |
| 1 | 1 | 11 | 11 | 10 | 2,1 | 3,1 | 3,6 |
| 2 | 2 | 12 | 12 | 11 | 2,2 | 3,2 | 3,7 |
| 3 | 3 | 13 | 13 | 12 | 2,3 | 3,3 | 3,8 |
| 4 | 4 | 14 | 14 | 13 | 2,4 | 3,4 | 3,9 |
| 5 | 5 | 15 | 15 | 14 | 2,5 | 3,5 | 4 |
| 6 | 6 | 16 | 16 | 15 | 2,6 | 3,6 | 4,1 |
| 7 | 7 | 17 | 17 | 16 | 2,7 | 3,7 | 4,2 |
| 8 | 8 | 18 | 18 | 17 | 2,8 | 3,8 | 4,3 |
| 9 | 9 | 19 | 19 | 18 | 2,9 | 3,9 | 4,4 |
| 0 | 10 | 20 | 20 | 19 | 3 | 4 | 4,5 |
| Е | Б | Г | В | Д | Е | А |
Рисунок 5 − Схемы к задаче 1
