Расчет статически неопределимой балки

       Балка прямоугольного сечения с отношением высоты к ширине   

  h / b = 2 из стали 20 нагружена силами, как показано  на рисунке 29.

       Данные взять из таблицы 10. Необходимо:

      1. Найти опорные реакции.

      2. Построить эпюры М и Q.

        3. Определить размеры сечения и округлить их до нормальных раз­меров.            

                                                                                                    Таблица 10

Данные к задаче 10

Номер	Схема	l	a 1 / а	a 2 / а	M	F	q
строки	по рис. 7	м			кНм	кН	кН/м
1	1	6,2	5	1	10	10	1
2	2	6	4	2	9	11	2
3	3	5,8	3	3	8	12	3
4	4	5,6	2	4	7	13	4
5	5	5,4	1	5	6	14	5
6	6	5,2	5	1	5	15	6
7	7	2	4	2	4	16	7
8	8	4,8	3	3	3	17	8
9	9	4,6	2	4	2	18	9
0	10	4,4	1	5	1	19	10
	Е	А	Д	Е	Б	Г	В

Задача 9

    Расчет статически неопределимой балки. Определение перемещений

    Используя     результаты,  полученные    в     задаче    8,   для балки,            

изображенной на рисунке 29, необходимо построить эпюру про­гибов.

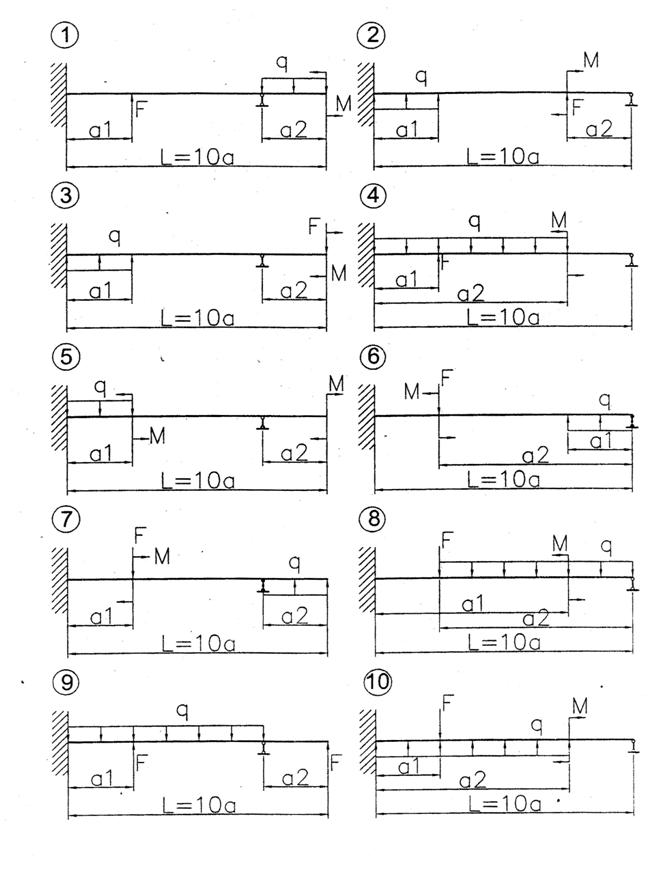
Рисунок 29 − Схемы балок к задаче 8

СЛОЖНОЕ СОПРОТИВЛЕНИЕ

             Сложное сопротивление — такой вид нагружения, при котором в поперечных сечениях бруса возникает два или больше внутренних усилий. Наиболее распространённые виды сложного сопротивления: кручение с изгибом, косой изгиб, внецентренное  растяжение или сжатие.

                  

Кручение и изгиб

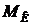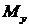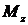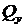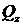Сочетание изгиба и кручения стержней круглого сечения чаще всего встречается при расчете валов. При одновременной деформации изгиба с кручением внутренние усилия в поперечном сечении стержня приводятся к пяти компонентам: крутящему моменту  относительно оси  (рисунок 30), изгибающим моментам   и  и поперечным силам  и . Нормальные напряжения достигают наибольшего значения в крайних волокнах стержня: точки А и В (рисунок 31), лежащих на концах диаметра, перпендикулярного к вектору результирующего изгибающего момента:

                 ; .                    

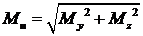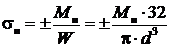
Касательные напряжения, определяющие 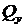 и 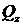, незначительны и их при расчете обычно не учитывают.

                      

                         Рисунок 30− Внутренние усилия в поперечном сечении

        при одновременном действии деформации изгиба с кручением

Касательные напряжения от кручения достигают максимального значения во всех точках контура сечения.

    , или 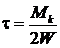, так как для круглого сечения W_p = 2∙ W

(W_p – полярный, W – осевой моменты инерции сечения).

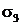В опасных точках А и В главные нормальные напряжения  и  определяют по формуле , а для проверки на прочность применяют одну из гипотез прочности.

  

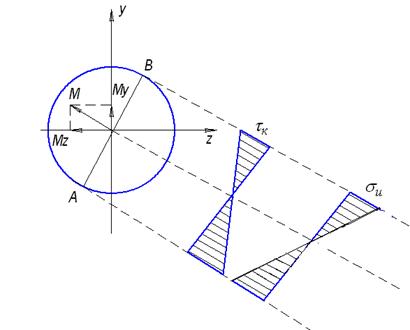
   Рисунок 31 − Распределение касательных и нормальных напряжений

                  в поперечном сечении стержня при изгибе с кручением

 

Для пластичных материалов пользуются третьей или четвертой гипотезой прочности:

                                                                      

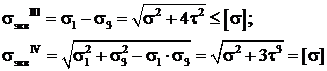
Выражая 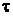 и 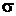 через крутящий и изгибающий моменты и подставляя значения главных напряжений в  для различных теорий прочности, расчетные формулы приведем к виду

                                                 ,                                           

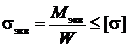где 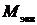– эквивалентный (расчетный) изгибающий момент:

          – по третьей теории прочности ;                       

       – по четвертой теории прочности ;