Решение дифференциальных уравнений с помощью

степенных рядов.

 

       С помощью степенных рядов возможно интегрировать дифференциальные уравнения.

       Рассмотрим линейное дифференциальное уравнение вида:

       Если все коэффициенты и правая часть этого уравнения разлагаются в сходящиеся в некотором интервале степенные ряды, то существует решение этого уравнения в некоторой малой окрестности нулевой точки, удовлетворяющее начальным условиям.

       Это решение можно представить степенным рядом:

       Для нахождения решения остается определить неизвестные постоянные c_i.

Эта задача решается методом сравнения неопределенных коэффициентов. Записанное выражение для искомой функции подставляем в исходное дифференциальное уравнение, выполняя при этом все необходимые действия со степенными рядами (дифференцирование, сложение, вычитание, умножение и пр.)

       Затем приравниваем коэффициенты при одинаковых степенях х в левой и правой частях уравнения. В результате с учетом начальных условий получим систему уравнений, из которой последовательно определяем коэффициенты c_i.

       Отметим, что этот метод применим и к нелинейным дифференциальным уравнениям.

 

       Пример. Найти решение уравнения c начальными условиями y (0)=1, y ’(0)=0.

Решение уравнения будем искать в виде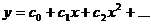

 

       Подставляем полученные выражения в исходное уравнение:

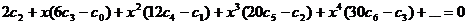
Отсюда получаем:

                              

                               ………………

Получаем, подставив начальные условия в выражения для искомой функции и ее первой производной:

Окончательно получим:

Итого:

 

 

       Существует и другой метод решения дифференциальных уравнений с помощью рядов. Он носит название метод последовательного дифференцирования.      

 

       Рассмотрим тот же пример. Решение дифференциального уравнения будем искать в виде разложения неизвестной функции в ряд Маклорена.

 

       Если заданные начальные условия y (0)=1, y ’(0)=0  подставить в исходное дифференциальное уравнение, получим, что

       Далее запишем дифференциальное уравнение в виде  и будем последовательно дифференцировать его по х.

 

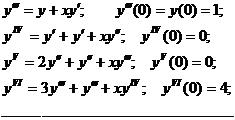
       После подстановки полученных значений получаем:

 

 

Ряды Фурье.

(Жан Батист Жозеф Фурье (1768 – 1830) – французский математик)

 

Тригонометрический ряд.

 

       Определение. Тригонометрическим рядом называется ряд вида:

или, короче,

       Действительные числа a_i, b_i называются коэффициентами тригонометрического ряда.

 

       Если ряд представленного выше типа сходится, то его сумма представляет собой периодическую функцию с периодом 2p, т.к. функции sin nx и cos nx также периодические функции с периодом 2p.

       Пусть тригонометрический ряд равномерно сходится на отрезке [-p; p], а следовательно, и на любом отрезке в силу периодичности, и его сумма равна f (x).

       Определим коэффициенты этого ряда.

 

       Для решения этой задачи воспользуемся следующими равенствами:

       Справедливость этих равенств вытекает из применения к подынтегральному выражению тригонометрических формул. Подробнее см. Интегрирование тригонометрических функций.

       Т.к. функция f (x) непрерывна на отрезке [-p; p], то существует интеграл

Такой результат получается в результате того, что .

Получаем:

 

Далее умножаем выражение разложения функции в ряд на cos nx и интегрируем в пределах от -p до p.

Отсюда получаем:

Аналогично умножаем выражение разложения функции в ряд на sin nx и интегрируем в пределах от -p до p.

Получаем:

 

Выражение для коэффициента а₀ является частным случаем для выражения коэффициентов a_n.

 

       Таким образом, если функция f (x) – любая периодическая функция периода 2p, непрерывная на отрезке [-p; p] или имеющая на этом отрезке конечное число точек разрыва первого рода, то коэффициенты

существуют и называются коэффициентами Фурье для функции f (x).

 

       Определение. Рядом Фурье для функции f (x) называется тригонометрический ряд, коэффициенты которого являются коэффициентами Фурье. Если ряд Фурье функции f (x) сходится к ней во всех ее точках непрерывности, то говорят, что функция f (x) разлагается в ряд Фурье.

 

 

Достаточные признаки разложимости в ряд Фурье.

 

       Теорема. (Теорема Дирихле) Если функция f (x) имеет период 2 p и на отрезке

[- p; p ] непрерывна или имеет конечное число точек разрыва первого рода, и отрезок

[- p; p ] можно разбить на конечное число отрезков так, что внутри каждого из них функция f (x) монотонна, то ряд Фурье для функции f (x) сходится при всех значениях х, причем в точках непрерывности функции f (x) его сумма равна f (x), а в точках разрыва его сумма равна , т.е. среднему арифметическому предельных значений слева и справа. При этом ряд Фурье функции f (x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f (x).

 

       Функция f(x), для которой выполняются условия теоремы Дирихле называется кусочно – монотонной на отрезке [-p;p].

 

       Теорема. Если функция f (x) имеет период 2 p, кроме того, f (x) и ее производная f ’(x) – непрерывные функции на отрезке [- p; p ] или имеют конечное число точек разрыва первого рода на этом отрезке, то ряд Фурье функции f (x) сходится при всех значениях х, причем в точках непрерывности его сумма равна f (x), а в точках разрыва она равна . При этом ряд Фурье функции f (x) сходится равномерно на любом отрезке, который принадлежит интервалу непрерывности функции f (x).

 

       Функция, удовлетворяющая условиям этой теоремы, называется кусочно – гладкой на отрезке [-p;p].

 

 

Разложение в ряд Фурье непериодической функции.

 

       Задача разложения непериодической функции в ряд Фурье в принципе не отличается от разложения в ряд Фурье периодической функции.

       Допустим, функция f (x) задана на отрезке [a, b] и является на этом отрезке кусочно – монотонной. Рассмотрим произвольную периодическую кусочно – монотонную функцию f ₁ (x) c периодом 2Т ³ ï b - a ï, совпадающую с функцией f(x) на отрезке [a, b].

 

                                                       y

                                                                   f(x)

 

 

                               a - 2T                a a     b a+2T         a + 4T        x

 

 

       Таким образом, функция f (x) была дополнена. Теперь функция f ₁ (x) разлагается в ряд Фурье. Сумма этого ряда во всех точках отрезка [a, b] совпадает с функцией f (x), т.е. можно считать, что функция f (x) разложена в ряд Фурье на отрезке [a, b].   

       Таким образом, если функция f(x) задана на отрезке, равном 2p ничем не отличается от разложения в ряд периодической функции. Если же отрезок, на котором задана функция, меньше, чем 2p, то функция продолжается на интервал (b, a + 2p) так, что условия разложимости в ряд Фурье сохранялись.

       Вообще говоря, в этом случае продолжение заданной функции на отрезок (интервал) длиной 2p может быть произведено бесконечным количеством способов, поэтому суммы получившихся рядов будут различны, но они будут совпадать с заданной функцией f(x) на отрезке [a,b].

 

 

Ряд Фурье для четных и нечетных функций.

           

       Отметим следующие свойства четных и нечетных функций:

1)

       2) Произведение двух четных и нечетных функций является четной функцией.

       3) Произведение четной и нечетной функций – нечетная функция.

 

Справедливость этих свойств может быть легко доказана исходя из определения четности и нечетности функций.

 

       Если f(x) – четная периодическая функция с периодом 2p, удовлетворяющая условиям разложимости в ряд Фурье, то можно записать:

 

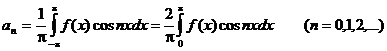
       Таким образом, для четной функции ряд Фурье записывается:

 

 

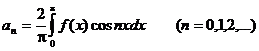
       Аналогично получаем разложение в ряд Фурье для нечетной функции:

 

 

       Пример. Разложить в ряд Фурье периодическую функцию  с периодом T = 2p на отрезке [-p;p].

       Заданная функция является нечетной, следовательно, коэффициенты Фурье ищем в виде:

 

 

 

 

 

 

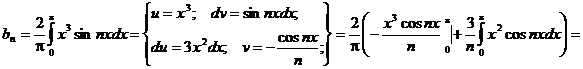
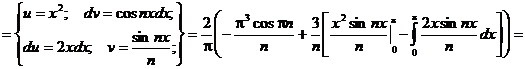
Получаем:

.

 

       Построим графики заданной функции и ее разложения в ряд Фурье, ограничившись первыми четырьмя членами ряда.

 

Ряды Фурье для функций любого периода.

 

       Ряд Фурье для функции f (x) периода Т = 2 l, непрерывной или имеющей конечное число точек разрыва первого рода на отрезке [- l, l ] имеет вид:

 

Для четной функции произвольного периода разложение в ряд Фурье имеет вид:

 

Для нечетной функции:

 

Ряд Фурье по ортогональной системе функций.

 

       Определение. Функции j(х) и y(х), определенные на отрезке [a, b], называются ортогональными на этом отрезке, если

 

       Определение. Последовательность функций j₁(x), j₂(x), …, jn(x), непрерывных на отрезке [a, b], называется ортогональной системой функций на этом отрезке, если все функции попарно ортогональны.

       Отметим, что ортогональность функций не подразумевает перпендикулярности графиков этих функций.

 

       Определение. Система функций называется ортогональной и нормированной (ортонормированной), если

 

       Определение. Рядом Фурье по ортогональной системе функций j₁(x), j₂(x), …,jn(x) называется ряд вида:

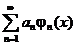
коэффициенты которого определяются по формуле:

,

где f (x) = 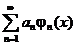 - сумма равномерно сходящегося на отрезке [a, b] ряда по ортогональной системе функций. f (x) – любая функция, непрерывная или имеющая конечное число точек разрыва первого рода на отрезке [a, b].

 

       В случае ортонормированной системы функций коэффициенты определяются:

 

 

       При использовании компьютерной версии “ Курса высшей математики ” возможно запустить программу, которая разлагает в ряд Фурье произвольную функцию.

           

 

Интеграл Фурье.

 

       Пусть функция f (x) на каждом отрезке [- l, l ], где l – любое число, кусочно – гладкая или кусочно – монотонная, кроме того, f (x) – абсолютно интегрируемая функция, т.е. сходится несобственный интеграл

 

       Тогда функция f (x) разлагается в ряд Фурье:

 

 

Если подставить коэффициенты в формулу для f(x), получим:

 

 

 

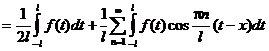
Переходя к пределу при l ® ¥, можно доказать, что  и

 

Обозначим  

При l ® ¥ D u_n ®0.