Пусть  квадратная матрица порядка
квадратная матрица порядка 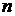 с действительными элементами. Пусть, с другой стороны,
с действительными элементами. Пусть, с другой стороны,  некоторое неизвестное. Тогда матрица (
некоторое неизвестное. Тогда матрица (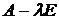 ), где
), где  единичная матрица порядка
единичная матрица порядка 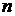 , называется характеристической матрицей матрицы
, называется характеристической матрицей матрицы  . Так как в матрице (
. Так как в матрице ( ) по главной диагонали стоит
) по главной диагонали стоит 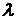 , все же остальные элементы равны нулю, то
, все же остальные элементы равны нулю, то

Определитель матрицы (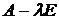 ) будет многочленом от
) будет многочленом от 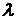 , притом степени
, притом степени 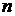 . В самом деле, произведение элементов, стоящих на главной диагонали, будет многочленом от
. В самом деле, произведение элементов, стоящих на главной диагонали, будет многочленом от 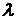 , со старшим членом
, со старшим членом  , все же остальные члены определителя не содержат по меньшей мере двух из числа элементов, стоящих на главной диагонали, и поэтому их степень относительно
, все же остальные члены определителя не содержат по меньшей мере двух из числа элементов, стоящих на главной диагонали, и поэтому их степень относительно 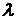 , не превосходит
, не превосходит  . Коэффициенты этого многочлена можно было бы легко найти. Так, коэффициент при
. Коэффициенты этого многочлена можно было бы легко найти. Так, коэффициент при  равен
равен  , а свободный член совпадает с определителем матрицы
, а свободный член совпадает с определителем матрицы  .
.
Многочлен  степени
степени  называется характеристическим многочленом матрицы
называется характеристическим многочленом матрицы  , а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
, а его корни, которые могут быть как действительными, так и комплексными, называются характеристическими корнями этой матрицы.
ТЕОРЕМА (о характеристических многочленах). Подобные матрицы обладают одинаковыми характеристическими многочленами и, следовательно, одинаковыми характеристическими корнями.
ДОКАЗАТЕЛЬСТВО. Пусть, в самом деле, 
 Тогда, учитывая, что матрица (
Тогда, учитывая, что матрица ( ) перестановочна с матрицей
) перестановочна с матрицей  , а
, а  получаем:
получаем:

что и требовалось доказать. □
Из этого результата вытекает, ввиду доказанной в §3.1 теоремы о связи матриц линейного оператора в разных базисах:
СЛЕДСТВИЕ. Линейный оператор  может задаваться в разных базисах различными матрицами, однако все эта матрицы имеют один и тот же набор характеристических корней. □
может задаваться в разных базисах различными матрицами, однако все эта матрицы имеют один и тот же набор характеристических корней. □
Эти корни можно называть поэтому характеристическими корнями самого оператора  . Весь набор этих характеристических корней, причем каждый корень берется с той кратностью, какую он имеет в характеристическом многочлене, называется спектром линейного оператора
. Весь набор этих характеристических корней, причем каждый корень берется с той кратностью, какую он имеет в характеристическом многочлене, называется спектром линейного оператора  .
.
Укажем одно из применений характеристических корней. Пусть в линейном пространстве  задан линейный оператор
задан линейный оператор  . Если вектор
. Если вектор  , отличный от нуля, переводится оператором
, отличный от нуля, переводится оператором  в вектор, пропорциональный самому
в вектор, пропорциональный самому  ,
,
 (6)
(6)
где  некоторое действительное число, то вектор
некоторое действительное число, то вектор  называется собственным вектором оператора
называется собственным вектором оператора  , а число
, а число  собственным значением этого оператора, причем говорят, что собственный вектор
собственным значением этого оператора, причем говорят, что собственный вектор  относится, к собственному значению
относится, к собственному значению 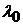 .
.
Заметим, что так как  , то число
, то число 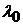 , удовлетворяющее условию (6), определяется для вектора
, удовлетворяющее условию (6), определяется для вектора  однозначно. Подчеркнем, далее, что нулевой вектор не считается собственным вектором оператора
однозначно. Подчеркнем, далее, что нулевой вектор не считается собственным вектором оператора  , хотя он удовлетворяет условию (6), притом для любого
, хотя он удовлетворяет условию (6), притом для любого 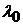 .
.
ТЕОРЕМА (о собственных значениях). Действительные характеристические корни линейного оператора  , если они существуют, и только они служат собственными значениями этого оператора.
, если они существуют, и только они служат собственными значениями этого оператора.
ДОКАЗАТЕЛЬСТВО. Пусть, в самом деле, оператор  имеет в базисе
имеет в базисе 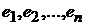 матрицу
матрицу  и пусть вектор
и пусть вектор

является собственным вектором оператора  ,
,
 (7)
(7)
Как доказано в §3.1,
 (8)
(8)
Равенства (7) и (8) приводят к системе равенств
 (9)
(9)
Так как  , то не все числа
, то не все числа  равны нулю. Таким образом, ввиду (9), система линейных однородных уравнений
равны нулю. Таким образом, ввиду (9), система линейных однородных уравнений
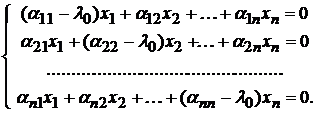 (10)
(10)
обладает ненулевым решением, а поэтому ее определитель равен нулю,
 (11)
(11)
или  т. е, собственное значение
т. е, собственное значение 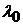 на самом деле оказалось характеристическим корнем матрицы
на самом деле оказалось характеристическим корнем матрицы  и, следовательно, линейного оператора
и, следовательно, линейного оператора  , притом, понятно, действительным.
, притом, понятно, действительным.
Обратно, пусть 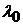 будет любым действительным характеристическим корнем оператора
будет любым действительным характеристическим корнем оператора  и, следовательно, матрицы
и, следовательно, матрицы  . Тогда имеет место равенство (11). Отсюда следует, что система линейных однородных уравнений (10) обладает ненулевым решением, притом даже действительным, так как все коэффициенты этой системы действительны. Если это решение обозначим через
. Тогда имеет место равенство (11). Отсюда следует, что система линейных однородных уравнений (10) обладает ненулевым решением, притом даже действительным, так как все коэффициенты этой системы действительны. Если это решение обозначим через
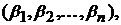 (12)
(12)
то имеют место равенства (9). Обозначим через  вектор пространства
вектор пространства  , имеющий в базисе
, имеющий в базисе  строку координат (12); ясно, что
строку координат (12); ясно, что  . Тогда справедливо равенство (8), а из (9) и (8) следует (7). Вектор
. Тогда справедливо равенство (8), а из (9) и (8) следует (7). Вектор  оказался, таким образом, собственным вектором оператора
оказался, таким образом, собственным вектором оператора  , относящимся к собственному значению
, относящимся к собственному значению 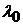 . Теорема доказана. □
. Теорема доказана. □
В заключении отметим, что совокупность собственных векторов линейного оператора  , относящихся к собственному значению
, относящихся к собственному значению 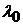 , совпадает с совокупностью ненулевых действительных решений системы линейных однородных уравнений (10). Отсюда следует, что совокупность собственных векторов линейного оператора
, совпадает с совокупностью ненулевых действительных решений системы линейных однородных уравнений (10). Отсюда следует, что совокупность собственных векторов линейного оператора  , относящихся к собственному значению
, относящихся к собственному значению 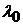 , будет, после добавления к ней нулевого вектора, линейным подпространством пространства
, будет, после добавления к ней нулевого вектора, линейным подпространством пространства  .
.
Пример 3. Найти собственные значения и собственные векторы линейного оператора, заданного в некотором базисе матрицей

Решение: Составим характеристическое уравнение
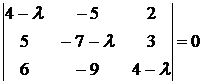 .
.
Раскрывая определитель, получим уравнение
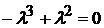 ,
,
корни которого  являются собственными значениями линейного оператора
являются собственными значениями линейного оператора  .
.
Найдём собственные векторы, соответствующие собственному значению  Для этого решим систему (10), считая
Для этого решим систему (10), считая 

После преобразования получим:
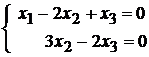 или
или 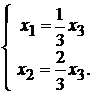
Фундаментальная система решений имеет вид:

| 
| 
|
| 1 | 2 | 3 |
Собственный вектор 
Аналогично, для  , получим систему линейных однородных уравнений
, получим систему линейных однородных уравнений

фундаментальным решением которой будет:

| 
| 
|
| 1 | 1 | 1 |
и  собственный вектор, соответствующий собственному значению
собственный вектор, соответствующий собственному значению 
ЗАДАЧИ К ГЛАВЕ III.
Векторы  и
и  заданы своими координатами в базисе
заданы своими координатами в базисе  . Показать, что векторы
. Показать, что векторы  сами образуют базис, и найти координаты вектора
сами образуют базис, и найти координаты вектора  в этом базисе:
в этом базисе:
110. 
111. 
112. 
113. 
114. 
115. 

Доказать, что системы векторов  и
и  образуют базис и найти матрицу перехода от одного базиса к другому:
образуют базис и найти матрицу перехода от одного базиса к другому:
116. 

117. 

Линейный оператор  в базисе
в базисе  имеет матрицу
имеет матрицу  , найти матрицу этого линейного оператора в базисе
, найти матрицу этого линейного оператора в базисе  :
:
118. 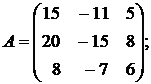

119. 

120. 
а)  ;
;
б) 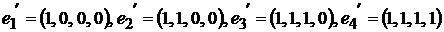 .
.
Найти собственные значения и собственные векторы линейных операторов, заданных в некотором базисе матрицами:
121. 
122. 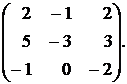
123. 
124. 
125. 
126. 
127. 
128. 
129. 
130. 
131. 
132. 
ГЛАВА 4.






