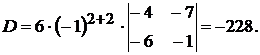Перестановкой из  чисел называется всякое расположение чисел от
чисел называется всякое расположение чисел от  до
до  в каком либо порядке. В общем виде она записывается так
в каком либо порядке. В общем виде она записывается так
 . (1)
. (1)
Говорят, что в перестановке (1) числа  и
и 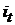 образуют инверсию, если
образуют инверсию, если  но
но  Перестановку называют чётной (нечётной), если количество всех её инверсий есть число чётное (соответственно нечётное). Оно обычно подсчитывается так: берём число
Перестановку называют чётной (нечётной), если количество всех её инверсий есть число чётное (соответственно нечётное). Оно обычно подсчитывается так: берём число  и находим количество чисел, лежащих правее и меньших
и находим количество чисел, лежащих правее и меньших  , т.е. число инверсий, которое образует
, т.е. число инверсий, которое образует  с остальными. Затем поступаем аналогично с числами
с остальными. Затем поступаем аналогично с числами 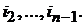 Сумма этих чисел и будет количеством всех её инверсий. Например, в перестановке 5, 3, 1, 4, 2 число инверсий равно 7 и поэтому она нечётная.
Сумма этих чисел и будет количеством всех её инверсий. Например, в перестановке 5, 3, 1, 4, 2 число инверсий равно 7 и поэтому она нечётная.
Если в перестановке поменять местами два элемента, то говорят, что в ней совершена транспозиция.
ЛЕММА (о транспозиции): При совершении одной транспозиции чётность перестановки изменяется.
ДОКАЗАТЕЛЬСТВО. Это почти очевидно, если в перестановке совершить транспозицию двух соседних элементов.
Предположим теперь, что совершена транспозиция в (1) элементов  и
и 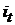 , где
, где  . Будем совершать транспозицию элемента
. Будем совершать транспозицию элемента 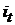 с
с 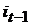 , затем с
, затем с 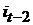 , пока
, пока 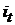 не займёт место элемента
не займёт место элемента  . При этом будет совершено
. При этом будет совершено  транспозиций соседних элементов. Затем совершаем транспозицию элемента
транспозиций соседних элементов. Затем совершаем транспозицию элемента  с
с 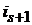 , затем с
, затем с 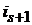 , пока
, пока  не займёт бывшее место элемента
не займёт бывшее место элемента 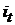 . При этом будет совершено
. При этом будет совершено 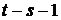 транспозиций, а всего
транспозиций, а всего 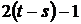 таких транспозиций. Это число нечётное, а поэтому чётность перестановки изменяется. □
таких транспозиций. Это число нечётное, а поэтому чётность перестановки изменяется. □
Правильным произведением квадратной матрицы  порядка
порядка 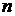 называется произведение
называется произведение 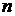 её элементов, никакие два из которых не лежат в одной и той же строке и столбце. Оно имеет вид
её элементов, никакие два из которых не лежат в одной и той же строке и столбце. Оно имеет вид
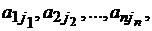 (2)
(2)
где 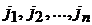 образуют перестановку из
образуют перестановку из 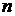 чисел. Эта перестановка называется соответствующей правильному произведению (2). Нетрудно убедиться, что количество правильных произведений (2) совпадает с количеством различных перестановок из
чисел. Эта перестановка называется соответствующей правильному произведению (2). Нетрудно убедиться, что количество правильных произведений (2) совпадает с количеством различных перестановок из 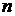 чисел и равно
чисел и равно 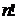 (факториал). Перейдём теперь к центральному понятию параграфа.
(факториал). Перейдём теперь к центральному понятию параграфа.
Определителем квадратной матрицы называется сумма всех её правильных произведений, причём каждое из них в этой сумме берётся со знаком «плюс», если соответствующая ему перестановка чётная, и со знаком «минус» – в противном случае.
Определитель матрицы  порядка
порядка 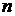 записывается так:
записывается так:
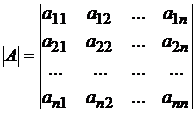
Непосредственно из определения следуют следующие свойства определителя.
Свойство 1. Определитель не меняется при транспонировании.
Из этого свойства вытекает, что утверждение, справедливое для строк, будет справедливым и для столбцов, и наоборот.
Свойство 2. Если одна из строк определителя состоит из нулей, то он равен нулю.
Свойство 3. При перестановке двух строк определитель меняет знак.
Свойство 4. Определитель, содержащий две одинаковые строки, равен нулю.
Свойство 5. Если все элементы некоторой строки определителя умножить на число 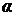 , то и определитель умножится на
, то и определитель умножится на 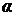 .
.
Свойство 6. Определитель, содержащий пропорциональные строки, равен нулю.
Свойство 7. Если в определителе 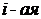 строка представима в виде
строка представима в виде
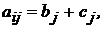

то он равен сумме двух определителей, у которых все строки, кроме 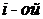 , равны строкам исходного определителя, а
, равны строкам исходного определителя, а 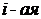 строка в одном из них есть
строка в одном из них есть  а в другом -
а в другом - 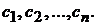
Свойство 8. Если в определителе одна из строк является линейной комбинацией двух других, то он равен нулю.
Свойство 9. Определитель не изменится, если к одной из его строк прибавить другую, умноженную на некоторое число.
Вообще, определитель не изменится, если к одной из его строк прибавить линейную комбинацию других строк.
Если в матрице зафиксировать 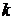 различных строк и столбцов, то на их пересечении элементы составят матрицу порядка
различных строк и столбцов, то на их пересечении элементы составят матрицу порядка 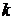 , определитель которой называется минором
, определитель которой называется минором  порядка этой матрицы. Если же исходная матрица квадратная и в ней вычеркнуть
порядка этой матрицы. Если же исходная матрица квадратная и в ней вычеркнуть 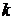 различных строк и столбцов с номерами
различных строк и столбцов с номерами 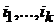 и
и 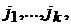 то определитель, составленный из элементов оставшихся
то определитель, составленный из элементов оставшихся 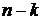 строк и столбцов, умноженный на число
строк и столбцов, умноженный на число 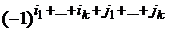 называется алгебраическим дополнением исходного минора
называется алгебраическим дополнением исходного минора  порядка.
порядка.
Доказательство следующей теоремы технически сложное и поэтому оно опускается.
ТЕОРЕМА ЛАПЛАСА. Зафиксируем в определителе 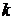 строк. Тогда сумма произведений всех миноров
строк. Тогда сумма произведений всех миноров  порядка, лежащих в этих фиксированных строках, на их алгебраические дополнения равна исходному определителю.
порядка, лежащих в этих фиксированных строках, на их алгебраические дополнения равна исходному определителю.
Так как один элемент 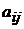 в квадратной матрице является минором первого порядка, то можно вычислить его алгебраическое дополнение, которое обозначается через
в квадратной матрице является минором первого порядка, то можно вычислить его алгебраическое дополнение, которое обозначается через 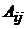 . Из теоремы Лапласа при
. Из теоремы Лапласа при 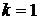 получаем
получаем
СЛЕДСТВИЕ 1. Сумма произведений всех элементов фиксированной строки определителя на их алгебраические дополнения равна определителю, т.е. 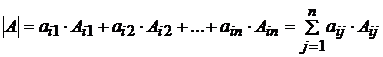 , при любом фиксированном
, при любом фиксированном 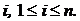 □
□
СЛЕДСТВИЕ 2. Сумма произведений всех элементов фиксированной строки определителя на соответствующие алгебраические элементы другой строки равна нулю, т.е. при 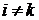
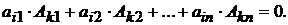 (3)
(3)
ДОКАЗАТЕЛЬСТВО. Заменим в исходном определителе 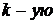 строку на
строку на 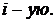 В полученном определителе две строки будут равными. Поэтому по свойству 4 он равен 0. Но, вычисляя его методом разложения по
В полученном определителе две строки будут равными. Поэтому по свойству 4 он равен 0. Но, вычисляя его методом разложения по 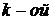 строке и используя следствие 1, как раз и получим сумму (3). □
строке и используя следствие 1, как раз и получим сумму (3). □
Разумеется, в теореме Лапласа и следствиях 1 и 2 слово «строки» можно заменить на слово «столбцы».
Матрица  называется треугольной, если все элементы над или под главной диагональю равны нулю. Непосредственно из определения определителя следует, что определитель треугольной матрицы равен произведению элементов его главной диагонали.
называется треугольной, если все элементы над или под главной диагональю равны нулю. Непосредственно из определения определителя следует, что определитель треугольной матрицы равен произведению элементов его главной диагонали.
Наконец, полезно запомнить правила вычислений определителей второго и третьего порядка. Именно,
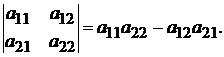
Пример 4.
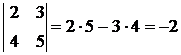 .
.

Чтобы запомнить, какие произведения в правой части равенства берутся со знаком ‹‹+››, а какие со знаком ‹‹-›› полезно использовать следующее правило треугольников:

Пример 5.
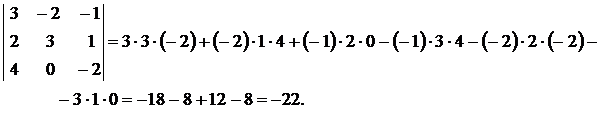
Для вычисления определителей более высоких порядков пользуются следующим алгоритмом: с помощью свойства 9 определителей добиваются того, чтобы в одной строке (или в одном столбце) все элементы за исключением одного равнялись нулю, затем по следствию 1 из теоремы Лапласа расписывают определитель по этой строке (столбцу). Тем самым вычисление определителя  сводят к вычислению определителя
сводят к вычислению определителя 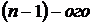 порядка. При необходимости процедуру повторяют.
порядка. При необходимости процедуру повторяют.
Пример 6. Вычислить определитель
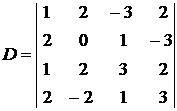 .
.
Решение. Домножив первую строку на (-2), (-1), (-2) и добавляя её соответственно ко второй, третьей и четвёртой строке, получим
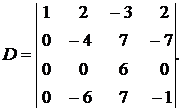
Распишем определитель по первому столбцу:
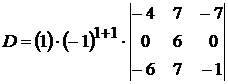 .
.
Расписывая полученный определитель третьего порядка по второй строке, получим