УДК 512.8
ББК
Д. И. Иванов. Алгебра (часть I): Учебно-методическое пособие по дисциплине "Алгебра" для студентов специальности "Компьютерная безопасность". Тюмень, 2008, 102 стр.
Данное пособие разработано в соответствии с государственным образовательным стандартом и учебным планом специальности "Компьютерная безопасность" (I семестр), содержит теоретическую часть и комплекс практических заданий.
Рекомендовано к печати Учебно-методической комиссией института математики и компьютерных наук. Одобрено Учебно-методической секцией Учёного совета Тюменского государственного университета.
ОТВЕТСТВЕННЫЙ РЕДАКТОР: В. Н. Кутрунов, д. ф.-м. н., профессор.
РЕЦЕНЗЕНТЫ: А. Н. Дёгтев, д. ф.-м. н., профессор кафедры алгебры и математической логики Тюменского государственного университета.
С. Д. Захаров, к. ф.-м. н., зав. каф. математики информатики и естественных наук Тюменского государственного института мировой экономики управления и права.
© ГОУ ВПО Тюменский государственный университет
© Д. И. Иванов, 2008
ВВЕДЕНИЕ.
ОСНОВНЫЕ МАТЕМАТИЧЕСКИЕ ПОНЯТИЯ.
Совокупность некоторых объектов (элементов) называют множеством. Пишут 
(
принадлежит 
), если 
элемент множества; 
означает, что не принадлежит множеству 
. Два множества, состоящие из одних и тех же элементов, называются равными. Множество, не содержащее ни одного элемента, называется пустым и обозначается символом 
. Если 
некоторое свойство, то через 
будем обозначать множество, элементами которого являются в точности все объекты, обладающие свойством . Например, пусть и 
множества. Тогда по определению:
объединение и ;
пересечение и ;
разность и .
Множество называется подмножеством множества 
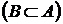, если каждый элемент множества является элементом множества .
Упорядоченный набор из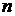 
элементов 
называется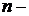 
кой (или кортежем)и обозначается 
. По определению равна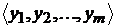 
, если 
и 
. Если 
> 1, непустые множества, то декартовым произведением их назовём множество
которое обозначается через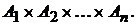 
В частности, 
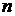( раз) обозначается через 
и называется декартовой степенью множества .
Подмножество 
множества 
называют 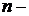местной функцией, заданной на со значениями во множестве , если из того, что 
и 
, следует, что 
(условие однозначности). Вместо пишут 
и говорят, что значение от 
определено (символически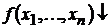 
) и равно 
. Множество
называется областью определения функции , а
называют областью значений .
Если 
, то функцию называют всюду определённой на , в противном случае - частичной. Если - одноместная всюду определённая на функция со значениями в , то называют отображением в и пишут 
Отображение в называют 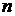-местной операцией, заданной на множестве .
Пусть дано Тогда отображение называют разнозначным (инъективным), если 
влечёт 
, отображением на (сюрьективным), если 
, и взаимнооднозначным (биективным),если оно одновременно инъективно и сюрьективно.
Если 
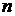-местная операция на , 
, причём 
для всех то называют замкнутым относительно .
ГЛАВА I.
МАТРИЦЫ И ОПРЕДЕЛИТЕЛИ.
