Пусть дано множество  ; его элементы будут обозначаться малыми латинскими буквами:
; его элементы будут обозначаться малыми латинскими буквами:  Пусть, далее, в множестве
Пусть, далее, в множестве  определены операция сложения, ставящая в соответствие всякой паре элементов
определены операция сложения, ставящая в соответствие всякой паре элементов  из
из  однозначно определенный элемент
однозначно определенный элемент 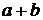 из
из  , называемый их суммой, и операция умножения на действительное число, причем произведение
, называемый их суммой, и операция умножения на действительное число, причем произведение  элемента
элемента  на число
на число 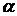 , однозначно определено и принадлежит к
, однозначно определено и принадлежит к  .
.
Элементы множества  будут называться векторами, а само
будут называться векторами, а само 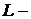 действительным линейным (или векторным, или аффинным) пространством, если указанные операции обладают свойствами
действительным линейным (или векторным, или аффинным) пространством, если указанные операции обладают свойствами  из §2.1. Так, арифметическое
из §2.1. Так, арифметическое 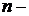 мерное векторное пространство является примером линейного пространства.
мерное векторное пространство является примером линейного пространства.
Два линейных пространства  и
и 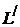 называются изоморфными, если существует биективное отображение
называются изоморфными, если существует биективное отображение 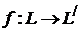 , ставящее в соответствие каждому вектору
, ставящее в соответствие каждому вектору  пространства
пространства  вектор
вектор  пространства
пространства 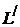 , такое что:
, такое что:

Пусть  базис
базис  и
и  . Так как
. Так как  система порождающих, то найдутся числа
система порождающих, то найдутся числа  такие, что
такие, что  . Если также
. Если также  , то имеем
, то имеем  . Но
. Но 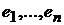 линейно независимая система, откуда
линейно независимая система, откуда  . Значит
. Значит  . Итак, представление вектора
. Итак, представление вектора  в виде линейной комбинации базисных векторов возможно и единственно. Набор (
в виде линейной комбинации базисных векторов возможно и единственно. Набор ( ) называется координатами вектора х в базисе
) называется координатами вектора х в базисе 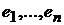 .
.
Отображение  называется линейным оператором, если выполнены условия: для всех
называется линейным оператором, если выполнены условия: для всех  и числа
и числа 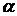 :
:
(а) 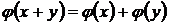
(б)  ,
,
которые можно заменить одним: для всех  и чисел
и чисел  верно
верно  . Отсюда следует равенство
. Отсюда следует равенство
 ,
,
широко используемое в дальнейшем.
Справедлива следующая
ТЕОРЕМА (о существовании и единственности  ). Пусть
). Пусть  базис
базис  и
и  произвольные векторы из
произвольные векторы из  . Тогда существует единственный линейный оператор
. Тогда существует единственный линейный оператор  такой, что
такой, что  .
.
ДОКАЗАТЕЛЬСТВО. Если 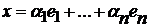 , то зададим
, то зададим  так:
так:  . Проверим, что
. Проверим, что  линейный оператор. Если
линейный оператор. Если  и
и  произвольные числа, то
произвольные числа, то 
Предположим, что  также линейный оператор
также линейный оператор  , причем
, причем  .
.
Имеем  . Итак
. Итак  для любого
для любого  . Значит
. Значит  . □
. □
Доказанная теорема показывает, что линейный оператор однозначно определяется в данном базисе 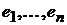 своими значениями
своими значениями  . Приходим к определению: матрицей линейного оператора
. Приходим к определению: матрицей линейного оператора  в базисе
в базисе 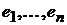 называется такая матрица
называется такая матрица 
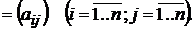 , у которой
, у которой  столбец есть координаты вектора
столбец есть координаты вектора  в базисе
в базисе 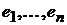 . Т. е.,
. Т. е.,
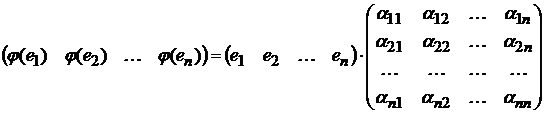 .
.
Обозначим через  столбец из координат вектора
столбец из координат вектора  в базисе
в базисе 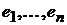 , т.е.
, т.е.  . В частности,
. В частности,  столбец из координат вектора
столбец из координат вектора  в этом же базисе.
в этом же базисе.
Имеет место следующее равенство
 (1)
(1)
Действительно, 
Но в последней сумме коэффициенты при 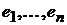 как раз есть координаты вектора
как раз есть координаты вектора  в базисе
в базисе 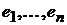 . Из правила умножения матрицы
. Из правила умножения матрицы  на столбец
на столбец  получаем искомое равенство (1). □
получаем искомое равенство (1). □
Пусть  другой базис L. Матрицей перехода от одного базиса
другой базис L. Матрицей перехода от одного базиса  к другому
к другому 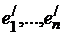 называется такая матрица
называется такая матрица 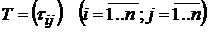 , у которой i -ый столбец есть координаты вектора
, у которой i -ый столбец есть координаты вектора  в базисе
в базисе  , т. е.
, т. е.

Фактически матрица  есть матрица линейного оператора, переводящего векторы
есть матрица линейного оператора, переводящего векторы  в
в 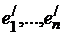 .
.
Пусть  столбец из координат вектора х в базисе
столбец из координат вектора х в базисе 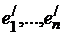 Тогда имеет место следующее равенство
Тогда имеет место следующее равенство
 (2)
(2)
Действительно, имеем

Но  откуда
откуда
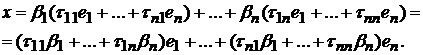
Но в последней сумме коэффициенты при  как раз и есть координаты вектора х в базисе
как раз и есть координаты вектора х в базисе  . Из правила умножения матрицы
. Из правила умножения матрицы  на столбец
на столбец  получаем (2).
получаем (2).
По следствию 2 из теоремы о ранге матриц 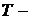 невырожденная матрица, т.к. её столбцы, будучи координатами базисных векторов линейно независимы. Поэтому Т имеет обратную матрицу
невырожденная матрица, т.к. её столбцы, будучи координатами базисных векторов линейно независимы. Поэтому Т имеет обратную матрицу  . Умножая обе части равенства (2) слева на
. Умножая обе части равенства (2) слева на  , получаем
, получаем

Пример 1.
Векторы  заданы своими координатами в некотором базисе
заданы своими координатами в некотором базисе  . Показать, что векторы
. Показать, что векторы 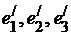 сами образуют базис, и найти координаты вектора x в этом базисе.
сами образуют базис, и найти координаты вектора x в этом базисе.
Решение. Составим матрицу перехода от базиса  к системе векторов
к системе векторов 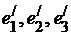 :
:
 ,
,
она невырожденная, значит векторы 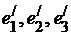 линейно независимы и могут образовывать базис трёхмерного пространства. Тогда
линейно независимы и могут образовывать базис трёхмерного пространства. Тогда

Найдём координаты вектора  в базисе
в базисе 

Следующая теорема устанавливает связь между матрицами одного и того же линейного оператора, заданными в разных базисах.
ТЕОРЕМА (о связи матриц линейного оператора). Пусть  и
и  – матрицы линейного оператора
– матрицы линейного оператора  в базисах
в базисах  и
и 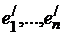 соответственно и
соответственно и 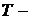 матрица перехода о первого базиса ко второму. Тогда
матрица перехода о первого базиса ко второму. Тогда  (матрицы
(матрицы  и
и  называются подобными).
называются подобными).
ДОКАЗАТЕЛЬСТВО. Если  , то обозначим через
, то обозначим через  и
и  столбцы из координат вектора
столбцы из координат вектора  в первом и во втором базисах, а через
в первом и во втором базисах, а через 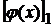 и
и  координаты образа этого вектора в первом и во втором базисах.. Из равенства (2) имеем
координаты образа этого вектора в первом и во втором базисах.. Из равенства (2) имеем
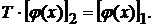
Из равенства (1) получаем
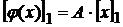 и
и  .
.
Из этих трех равенств заключаем, что
 .
.
Но 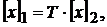 откуда
откуда
 .
.
Домножая обе части этого равенства на  слева, получаем равенство
слева, получаем равенство
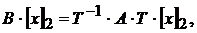
Которое имеет место при любом векторе  . Это означает равенство матриц
. Это означает равенство матриц  и
и  . □
. □
В доказательстве теоремы молчаливо использовался тот факт, что если для любого вектора х выполнено  , то
, то  . Предлагается его доказать читателю.
. Предлагается его доказать читателю.
Пример 2. Линейный оператор  в базисе
в базисе  имеет матрицу
имеет матрицу  . Найти его матрицу
. Найти его матрицу  в базисе
в базисе

Решение. Составим матрицу перехода от базиса  к базису
к базису 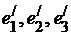 :
:

Найдём обратную матрицу для  :
:
 .
.
Тогда







