Для доказательства основной теоремы этого параграфа потребуется понятие прямой суммы подпространств.
Пусть  и
и 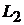 – два подпространства линейного пространства
– два подпространства линейного пространства  . Их суммой
. Их суммой  называется множество всех векторов
называется множество всех векторов 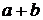 , где
, где  и
и  , т.е.
, т.е. 
Легко проверить, что  также будет подпространством L.
также будет подпространством L.
Сумма  называется прямой, если из того, что
называется прямой, если из того, что  , где
, где  и
и  следует, что
следует, что  и
и  .
.
Определим также и пересечение двух подпространств  которое также будет подпространством
которое также будет подпространством  . Именно
. Именно
 и
и 
ТЕОРЕМА (о прямых суммах подпространств). Сумма подпространств  и
и 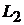 будет прямой тогда и только тогда, когда
будет прямой тогда и только тогда, когда  .
.
ДОКАЗАТЕЛЬСТВО. Пусть  – прямая сумма подпространств
– прямая сумма подпространств  и
и 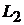 , но есть вектор
, но есть вектор  такой, что
такой, что 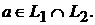 Тогда, так как
Тогда, так как  также является подпространством, то
также является подпространством, то  , и получается, что нулевой вектор можно представить двумя различными способами
, и получается, что нулевой вектор можно представить двумя различными способами  . Таким образом, приходим к противоречию определения прямой суммы.
. Таким образом, приходим к противоречию определения прямой суммы.
Обратно, пусть  , но сумма
, но сумма  не прямая. Значит найдется
не прямая. Значит найдется  и
и  такие, что
такие, что  , но
, но  Так как
Так как  и
и 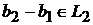 , то
, то  содержит ненулевой вектор
содержит ненулевой вектор  Опять приходим к противоречию. □
Опять приходим к противоречию. □
ТЕОРЕМА (о размерности суммы двух подпространств). Размерность суммы двух подпространств пространства  равна сумме их размерностей минус размерность их пересечения.
равна сумме их размерностей минус размерность их пересечения.
ДОКАЗАТЕЛЬСТВО. Пусть  и
и 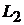 – подпространства,
– подпространства, 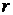 и
и  их размерности, а
их размерности, а  размерность их пересечения. Рассмотрим некоторый базис
размерность их пересечения. Рассмотрим некоторый базис  , скажем
, скажем 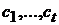 , и дополним его до базисов
, и дополним его до базисов  и
и  пространств
пространств  и
и 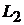 .
.
Докажем, что система
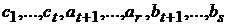 , (3)
, (3)
состоящая из  векторов является базисом подпространства
векторов является базисом подпространства  , тем самым будет доказана и теорема.
, тем самым будет доказана и теорема.
Ясно, что любой вектор  и
и  , а значит и вектор
, а значит и вектор  линейно выражается через векторы системы (3), т.к. содержит базисы
линейно выражается через векторы системы (3), т.к. содержит базисы  и
и 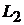 . Осталось проверить, что система (3) линейно независима. Предположим, что
. Осталось проверить, что система (3) линейно независима. Предположим, что
 (4)
(4)
Пусть  Понятно, что
Понятно, что  . Но
. Но
 . (5)
. (5)
Правая часть этого равенства есть вектор из  , т.е.
, т.е.  . Окончательно,
. Окончательно,  . Значит в выражении (5) отсутствуют члены с
. Значит в выражении (5) отсутствуют члены с 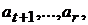 т.е.
т.е.  . Отсюда и из (4) заключаем, что
. Отсюда и из (4) заключаем, что
 .
.
Так как система  является базисом
является базисом 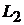 , то она линейно независима и поэтому
, то она линейно независима и поэтому  □
□
Если сумма  прямая, то размерность
прямая, то размерность  по теореме о прямых суммах равна 0, и поэтому получаем
по теореме о прямых суммах равна 0, и поэтому получаем
СЛЕДСТВИЕ. Размерность прямой суммы двух подпространств равна сумме их размерностей. □
Пусть  линейный оператор
линейный оператор  и
и

Нетрудно проверить, что  и
и  подпространства
подпространства  , называемые областью значений и ядром линейного оператора
, называемые областью значений и ядром линейного оператора  . Размерность
. Размерность  называется рангом, а размерность
называется рангом, а размерность  дефектом
дефектом  .
.
ТЕОРЕМА (о ранге и дефекте). Сумма ранга и дефекта линейного оператора φ равна размерности пространства  .
.
ДОКАЗАТНЛЬСТВО. Пусть 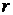 и
и  ранг и дефект
ранг и дефект  . Выберем в
. Выберем в  базис
базис  и обозначим через
и обозначим через  векторы такие, что
векторы такие, что 
Они линейно независимы, т.к. из равенства  следует, что
следует, что  а поскольку
а поскольку  линейно независимы, то
линейно независимы, то 
Обозначим через 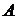 подпространство, порожденное векторами
подпространство, порожденное векторами  Они образуют базис
Они образуют базис 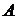 и поэтому размерность подпространства
и поэтому размерность подпространства 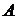 равна
равна 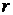 . По предыдущему следствию достаточно теперь доказать, что
. По предыдущему следствию достаточно теперь доказать, что  является прямой суммой
является прямой суммой 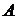 и
и  . покажем, что
. покажем, что  Любой вектор
Любой вектор  имеет вид
имеет вид  Если
Если 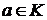 , то
, то  , т.е.
, т.е.  . Но векторы
. Но векторы  линейно независимы и поэтому
линейно независимы и поэтому  , откуда
, откуда  .
.
Покажем теперь, что  . Возьмем вектор
. Возьмем вектор  . Но
. Но  и поэтому
и поэтому  Пусть
Пусть  и
и  . Так как
. Так как  , то
, то  . Следовательно
. Следовательно  . Имеем
. Имеем  , где
, где  и
и  , что и требовалось доказать. □
, что и требовалось доказать. □






