Общий вид СЛУ задается системой:
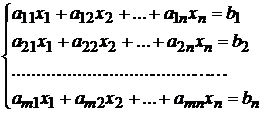 (*)
(*)
Набор чисел 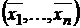 такой, который при подстановке вместо
такой, который при подстановке вместо  , каждое из уравнений системы обращает в тождество, называется ее частным решением. Найти общее решение СЛУ, значит указать метод, позволяющий получить все частные ее решения. СЛУ называется совместной, если она имеет хотя бы одно частное решение, и несовместной – иначе.
, каждое из уравнений системы обращает в тождество, называется ее частным решением. Найти общее решение СЛУ, значит указать метод, позволяющий получить все частные ее решения. СЛУ называется совместной, если она имеет хотя бы одно частное решение, и несовместной – иначе.
Классической является следующая
ТЕОРЕМА КРОНЕКЕРА – КАПЕЛЛИ. Система линейных уравнений совместна тогда и только тогда, когда ранг ее основной матрицы равен рангу расширенной.
ДОКАЗАТЕЛЬСТВО. Пусть СЛУ (*) имеет частное решение 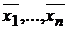 . Видно, что столбец из свободных членов СЛУ является линейной комбинацией столбцов ее основной матрицы. Поэтому ранг основной матрицы равен рангу расширенной.
. Видно, что столбец из свободных членов СЛУ является линейной комбинацией столбцов ее основной матрицы. Поэтому ранг основной матрицы равен рангу расширенной.
Обратно, пусть ранг основной матрицы СЛУ равен рангу расширенной. С точностью до перестановки уравнений и переименования неизвестных можно считать, что минор наивысшего порядка r находится на пересечении первых r строк и столбцов основной матрицы. Следовательно, существуют такие числа 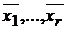 , что столбец из свободных членов равен линейной комбинации первых
, что столбец из свободных членов равен линейной комбинации первых 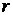 столбцов основной матрицы. Полагая
столбцов основной матрицы. Полагая  , видно, что
, видно, что 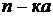 (
( ) является решением
) является решением
СЛУ (*). □
Две СЛУ от одного и того же числа неизвестных называются равносильными, если они обе не совместны, либо множества их частных решений равны. Нетрудно показать, что полученная СЛУ равносильна исходной, если
- из СЛУ вычеркнуть уравнение вида  ;
;
- обе части какого-то уравнения СЛУ умножить на число, отличное от нуля;
- прибавить к одному из уравнений другое, умноженное на некоторое число.
Изложим один метод решения СЛУ (*), называемый методом последовательного исключения переменных (или методом Гаусса). Будем считать, что 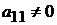 (этого можно всегда добиться с помощью перестановок строк). Попытаемся теперь, умножая первое уравнение на подходящие числа и прибавляя его к последующим, уничтожить в них слагаемые, содержащие
(этого можно всегда добиться с помощью перестановок строк). Попытаемся теперь, умножая первое уравнение на подходящие числа и прибавляя его к последующим, уничтожить в них слагаемые, содержащие 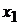 . Для этого, умножаем первое уравнение на
. Для этого, умножаем первое уравнение на 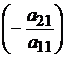 и прибавляем ко второму, и так далее, пока не умножим первое уравнение на
и прибавляем ко второму, и так далее, пока не умножим первое уравнение на  и не прибавим к последнему. Получим равносильную СЛУ вида
и не прибавим к последнему. Получим равносильную СЛУ вида

Полагаем, что  (этого можно добиться, переставляя строки или переименовывая переменные). Затем временно «забываем» про первое уравнение и продолжаем такую процедуру с оставшимися. Если в результате этой процедуры возникнет уравнение вида
(этого можно добиться, переставляя строки или переименовывая переменные). Затем временно «забываем» про первое уравнение и продолжаем такую процедуру с оставшимися. Если в результате этой процедуры возникнет уравнение вида  и
и 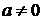 , то система несовместна, если же одно из уравнений окажется вида
, то система несовместна, если же одно из уравнений окажется вида  , то это уравнение можно опустить. В результата придем к ступенчатой СЛУ, которая имеет вид
, то это уравнение можно опустить. В результата придем к ступенчатой СЛУ, которая имеет вид
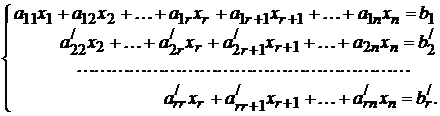
Эта часть метода Гаусса часто носит название «прямого хода». Заметим, что число 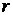 является рангом основной матрицы СЛУ и он равен рангу расширенной. Теперь для нахождения общего решения СЛУ (*) воспользуемся «обратным ходом». Для этого из последнего уравнения системы выразим
является рангом основной матрицы СЛУ и он равен рангу расширенной. Теперь для нахождения общего решения СЛУ (*) воспользуемся «обратным ходом». Для этого из последнего уравнения системы выразим 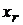 через
через 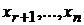 . Зная это выражение из предпоследнего уравнения можно выразить
. Зная это выражение из предпоследнего уравнения можно выразить 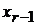 также через
также через 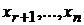 , и так далее. Наконец получим систему
, и так далее. Наконец получим систему
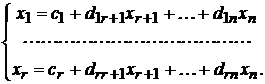
Она равносильна исходной и называется общим решением СЛУ (*). Теперь подставляя вместо неизвестных произвольные значения  и вычисляя
и вычисляя 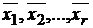 можно получить все частные решения (
можно получить все частные решения ( ) СЛУ (*).
) СЛУ (*).
Пример 3. Решить систему уравнений

Решение. Подвергнем преобразованиям расширенную матрицу этой системы:
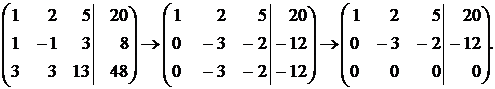
Ранг основной матрицы системы равен рангу расширенной матрицы и равен двум. Приходим, следовательно, к системе уравнений, равносильной исходной
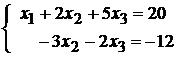 ,
,
в которой одна переменная является независимой. В качестве независимой переменной возьмём  , и выразим через неё остальные, получим:
, и выразим через неё остальные, получим:
 .
.
Полагая, например, 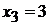 , получим одно из частных решений системы:
, получим одно из частных решений системы:

Если все свободные члены СЛУ 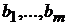 равны
равны  , то СЛУ называется системой линейных однородных уравнений (СЛОУ). СЛОУ всегда имеет тривиальное (нулевое) решение
, то СЛУ называется системой линейных однородных уравнений (СЛОУ). СЛОУ всегда имеет тривиальное (нулевое) решение 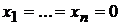 . Несложно проверить истинность следующих утверждений:
. Несложно проверить истинность следующих утверждений:
- сумма двух частных решений СЛОУ также является ее частным решением;
- если число умножить на частное решение СЛОУ, то получится также ее частное решение.
В частности, если СЛОУ зависит от n неизвестных, то множество всех частных решений ее образует подпространство в пространстве  . Базис этого подпространства называется фундаментальной системой решений СЛОУ.
. Базис этого подпространства называется фундаментальной системой решений СЛОУ.
ТЕОРЕМА(о СЛОУ). Фундаментальная система решений СЛОУ состоит из  некоторых ее частных решений, где
некоторых ее частных решений, где 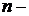 число неизвестных СЛОУ, а
число неизвестных СЛОУ, а 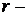 ранг ее основной матрицы.
ранг ее основной матрицы.
ДОКАЗАТЕЛЬСТВО.Рассмотрим СЛОУ (*), считая, что 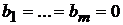 . Найдем ее общее решение, которое будет иметь вид
. Найдем ее общее решение, которое будет иметь вид
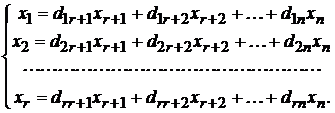

Далее свободным неизвестным 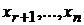 будем приписывать последовательно
будем приписывать последовательно  , а всем остальным
, а всем остальным  . Получим
. Получим  частных решений, которые сведем в следующую таблицу
частных решений, которые сведем в следующую таблицу
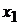
| 
| 
| 
| 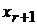
| 
| 
| 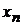
|
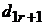
| 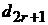
| 
| 
| 1 | 0 | 
| 0 |

| 
| 
| 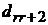
| 0 | 1 | 
| 0 |

| 
| 
| 
| 
| 
| 
| 
|

| 
| 
| 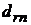
| 0 | 0 | 
| 1 |
Покажем, что векторы 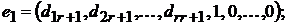
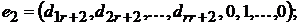
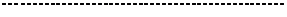
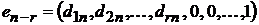
образуют фундаментальную систему СЛОУ (*).
Минор, стоящий на пересечении всех ее решений и последних их  столбцов не равен
столбцов не равен  . Значит, решения линейно независимы. Пусть теперь
. Значит, решения линейно независимы. Пусть теперь 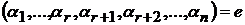 какое-то ее частное решение. Докажем, что вектор
какое-то ее частное решение. Докажем, что вектор 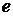 линейно выражается через векторы
линейно выражается через векторы 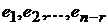 . Рассмотрим линейную комбинацию
. Рассмотрим линейную комбинацию 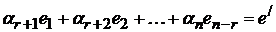 , вектор
, вектор 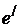 тоже является решением СЛОУ. Имеем,
тоже является решением СЛОУ. Имеем, 
 . Но
. Но 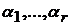 и
и  однозначно определяются в общем решении через значения
однозначно определяются в общем решении через значения 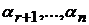 , придаваемых свободным неизвестным. Поэтому
, придаваемых свободным неизвестным. Поэтому 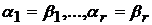 . Таким образом, векторы
. Таким образом, векторы 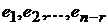 являются и системой порождающих подпространства решений СЛОУ, т.е. ее базисом. □
являются и системой порождающих подпространства решений СЛОУ, т.е. ее базисом. □
СЛЕДСТВИЕ. СЛОУ имеет тривиальное решение в том и только в том случае, когда ранг ее основной матрицы равен числу неизвестных. □
Таблица, приведенная выше, позволяет практически находить фундаментальную систему решений СЛОУ, чем должно заканчиваться ее решение.
Пример 4. Решить систему

Решение. Это система однородных уравнений, причём число уравнений меньше числа неизвестных; она будет иметь множество решений. Так как все свободные члены равны нулю, то будем подвергать преобразованиям лишь матрицу из коэффициентов системы:

Мы пришли к системе уравнений

В качестве независимых выберем две переменные, например  . Выразим остальные переменные через независимые. Получим
. Выразим остальные переменные через независимые. Получим
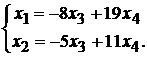
Тогда фундаментальная система будет иметь следующий вид:
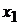
| 
| 
| 
|
| -8 | -5 | 1 | 0 |
| 19 | 11 | 0 | 1 |
Любое частное решение системы может быть представлено в виде линейной комбинации фундаментальных решений, т. е. общее решение системы

ЗАДАЧИ К ГЛАВЕ II.
Найти ранг следующих матриц методом окаймления миноров:
78. 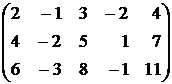
79. 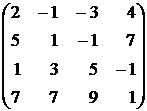
80. 
Вычислить ранг следующих матриц при помощи элементарных преобразований:
81. 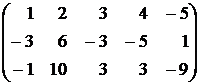
82. 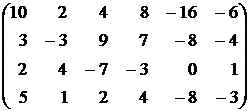
83. 
84. 
85. 
86. 
Определить ранг матриц при различных значениях 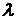 :
:
87. 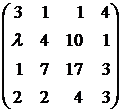
88. 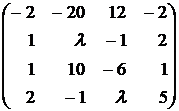
Исследовать совместность и найти общее и одно частное решение системы уравнений:
89. 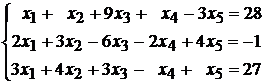
90. 
91. 
92. 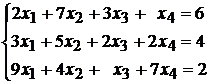
93. 
94. 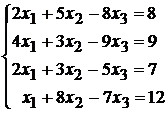
95. 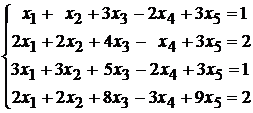
96. 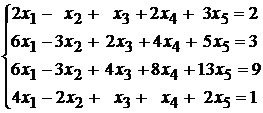
97. 
98. 
99. 
Исследовать систему и найти общее решение в зависимости от значений параметра:
100.
101. 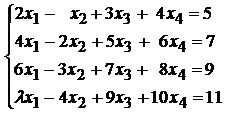
Найти общее решение и фундаментальную систему решений для систем уравнений:
102. 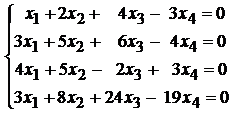
103. 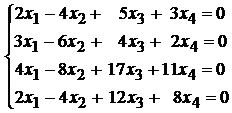
104. 
105. 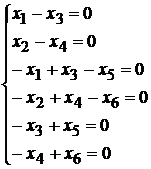
106. 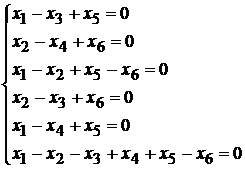
107. 
108. 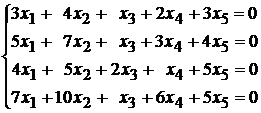
109. Какие из строк матрицы
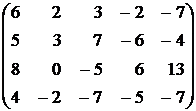
образуют фундаментальную систему решений для системы уравнений

ГЛАВА 3.
ЛИНЕЙНЫЕ ОПЕРАТОРЫ.






