1. Ввести заголовок (рис. 17).
2. Ввести прямоугольные матрицы M и N с произвольными элементами, состоящие, например, из 2 строк и 3 столбцов. Задать имена соответствующим диапазонам.
3. Поэлементные операции — это действия, которые выполняются над соответствующими элементами матриц.
Рис. 17. Образец работы
3.1. Вычислить сумму двух матриц. Ввести заголовок. Под заголовком выделить диапазон для результата (такой же, как матрицы). Ввести =М+N и нажать {Ctrl+Shift+Enter} — точно так же, как для векторов.
3.2. Вычислить поэлементное произведение двух матриц. Ввести заголовок. Под заголовком выделить диапазон для результата (такой же, как матрицы). Ввести =М*N и нажать {Ctrl+Shift+Enter}.
4. Транспонированиематрицы — это операция над матрицей, при которой строки и столбцы меняются местами без изменения порядка. Ввести заголовок. Выделить диапазон для матрицы 
, состоящий из 3 строк и 2 столбцов. Ввести формулу =ТРАНСП(N) (с помощью кнопки 
«Вставить функцию» в категории «Ссылки и массивы» или ввести с клавиатуры) и нажать {Ctrl+Shift+Enter}. Задать имя для диапазона.
5. Вычислить произведение матриц по правилу матричного умножения.
5.1. Ввести заголовок M*L. Выделить диапазон для результата умножения: количество строк — как в первой матрице, количество столбцов — как во второй. Ввести формулу =МУМНОЖ(M;L) (в категории «Математические» под кнопкой 
) и нажать {Ctrl+Shift+Enter}. Проверить получившийся результат.
5.2. Ввести заголовок L*M. Выделить нужный диапазон, ввести формулу =МУМНОЖ(L;M) и нажать {Ctrl+Shift+Enter }. Проверить результат.
6. Найти максимальный и минимальный элемент матрицы М. Ввести заголовок. Ввести в ячейку =МАКС(M) или =МИН(M) и нажать {Enter} — как для обычной функции. Если функции вводятся с клавиатуры, не забыть заменить язык ввода, имя М — это латиница.
Замечания:
– вычисления с матрицами удобно производить с помощью формул массива: для результата выделить диапазон, ввести формулу и нажать {Ctrl+Shift+Enter};
– матричное умножение выполняется матричной функцией МУМНОЖ;
– поэлементное умножение выполняется, как обычное умножение.
РАБОТА 3_3. Вычисление выражений с матрицами
ЗАДАНИЕ А
Ввести матрицы A, B и C и вычислить значение заданного выражения.
Указания. По смыслу задания умножение здесь матричное, следовательно, выполняется матричной функцией МУМНОЖ. Разбить выражение на блоки, чтобы одновременно перемножать только две матрицы, во избежание ошибок со скобками.
На примере возведения матрицы в степень:
| Формула | Название блока | Введённый текст |
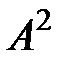
| F | =МУМНОЖ(A;A) |
| G | =МУМНОЖ(F;A) |
|
| G | =МУМНОЖ(МУМНОЖ(A;A);A) |
| H | =МУМНОЖ(F;F) |
