Основы выборочного метода. Методы отбора. Понятие репрезентативности выборки. Генеральное и выборочное среднее, генеральная и выборочная дисперсия

 

Научная дисциплина, разрабатывающая и систематизирующая понятия, приемы, математические методы и модели, предназначенные для организации сбора, систематизации и обработки данных в целях их интерпретации и получения выводов, называется анализом данных или прикладной статистикой.

Пусть проводится некоторый опыт (рассматривается некоторое явление). Все возможные (говорят, мысленные) результаты измерений или опыта образуют так называемую генеральную совокупность. Свойства и характеристики генеральной совокупности обычно неизвестны, а зачастую, и не могут быть определены. Для оценки этих свойств и характеристик используют выборочную совокупность или выборку, которая является совокупностью случайно выбранных объектов, т.е. полученных в результате конечного числа измерений. Необходимо, исследуя данные выборки, как можно точнее оценить свойства и характеристики генеральной совокупности. Решение такого рода задач - предмет рассмотрения дисциплины называемой математической статистикой. Отметим, что она применима только к массовым явлениям, имеющим вероятностную природу.

Вместе с тем, встречается множество ситуаций, когда полученные данные, даже если их и много, характеризуют не все, а только некоторые объекты. В таких случаях мы не всегда вправе распространять результаты обработки данных на другие (не рассмотренные) объекты. Например, проведено обследование приморских городов страны. Полученные характеристики будут справедливы только для этих городов и не могут быть в полной мере распространены на города, расположенные в глубинных районах. Другой пример: проведено исследование населения городов с числом жителей более миллиона. Полученные данные нельзя использовать для прогнозирования ситуации в населенных пунктах с другой численностью населения. Или в 12 часов дня проведен опрос населения по домашним телефонам, хотя в это время основная масса трудоспособного населения не находится дома. Данные опроса нельзя распространить на всех жителей города. 

Основной целью применения аппарата математической статистики является оценка некоторых характеристик генеральной совокупности по данным выборки, например, математического ожидания и дисперсии или ее закона распределения в целом с тем, чтобы иметь возможность при решении прикладных задач применять аппарат теории вероятностей.

Поскольку рассматривается только выборка (а не генеральная совокупность), при решении задач математической статистики всегда присутствует элемент случайности, и результаты получаются лишь с некоторой степенью уверенности.

Существуют разные способы отбора выборок. Прежде всего, отбор бывает бесповторным – элемент отбирает, его характеристики записываются и он не возвращается в генеральную совокупность – и повторным, когда элемент возвращается в генеральную совокупность и может быть отобран снова.

Первый способ важен, например, при контроле продукции, если контроль приводит к повреждению изделия или при социологических опросах, так как нельзя опрашивать дважды одного и того же человека.

В любом случае, при очень большом объеме генеральной совокупности и при малом объеме выборки разница между этими двумя способами отбора стирается.

В любом случае выборка должна правильно представлять все пропорции генеральной совокупности, т.е. быть репрезентативной. Выборка будет репрезентативной, если проводится случайный отбор, когда все элементы генеральной совокупности могут попасть в выборку с равной вероятностью.

На практике применяют следующие способы отбора.

В первом случае генеральная совокупность не делится на части и производится простой случайный отбор, который может быть повторным или бесповторным.

Во втором случае генеральная совокупность делится на части. При этом может быть типический, механический или серийный отбор.

При типическом отборе генеральная совокупность делится на типические части и из каждой части отбор производится отдельно. Пример: выборы по сословному признаку в органы управления.

При механическом отборе отбирают определенный объем генеральной совокупности, например 20%, и тогда отбирается каждый пятый объект и т.д. При этом правило репрезентативности может не выполнятся.

При серийном отборе объекты отбираются не по одному, а сериями. Используют при малой изменчивости исследуемого признака.

На практике часто применяют комплексный отбор.

 

Первичная обработка данных. Решение любой задачи математической статистики предваряет первичная обработка наблюдений. Пусть из генеральной совокупности в результате проведения в одинаковых условиях независимых опытов получено n значения исследуемой случайной величины X. Это значит, что получена выборка объема n. Наблюдаемые значения называют вариантами, последовательность вариант, записанных в возрастающем порядке ˗ вариационным рядом или статистической совокупностью. Данные записывают в виде таблицы, где в первой строчке пишутся варианты, а во второй строчке частоты 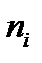– количество повторений данной варианты или относительные частоты 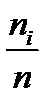. Такую таблицу называют статистическим распределением выборки (табл. 1)

 

Таблица 1. Статистическое распределение выборки

Варианты xi	x 1	x 2	x 3	...	x m
Частоты ni	n 1	n 2	n 3	…	nm

 

 

Графическое изображение статистического ряда называется полигоном частот (или относительных частот (рис. 1. 1))

 

Рис. 1.1. Полигон частот

 

Если получено большое число данных, а в статистике оперируют, как правило, сотнями и тысячами значений, то их группируют. Для этого весь диапазон полученных значений случайной величины X разбивают на разряды (подинтервалы). Для удобства обычно вводят k = 5 - 10 максимум 20 разрядов (большее число разрядов сложно анализировать, а при малом их числе происходит излишнее огрубление исследуемых зависимостей). В каждом конкретном случае число интервалов определяется исследователем в зависимости от размера выборки. При этом надо учесть, что чем меньше групп, тем больше потеря информации и чем меньше количество вариант в группе, тем менее надежны выводы. Ориентировочно количество интервалов k задается эмпирической формулой

 

.

 

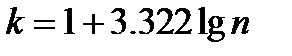Для каждого разряда подсчитывается число попавших в него значений k _i из выборки. Если каждое из k _i разделить на общее количество данных n в выборке, то получим относительные частоты попадания в соответствующий разряд (здесь и далее знак ^* говорит о том, что это статистический аналог соответствующего понятия теории вероятностей). Полученные таким образом данные образуют табл. 2, также называемую статистическим рядом,

 

Таблица 2. Статистическое распределение сгруппированной выборки

интервалы	x0-x1	x1-x2	...	xk-1-xk
частоты ki	k 1	k 2	...	km
Относительные частоты pi *	p 1*	p 2*	...	p m *

 

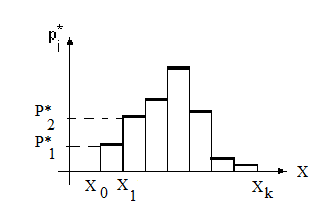
Рис.1.2.       Рис. 1.3. Статистическая функция   

Гистограммараспределения

 

после чего строится график, который называется гистограмма (рис. 1.2). По горизонтальной оси откладываются интервалы, а по вертикальной ˗ частоты.Данные статистического ряда можно использовать для построения статистической функции распределения

 

F ^*(x) = P ^*(X < x).

 

График этой функции, изображенной на рис.1.3, всегда представляет собой характерную ступенчатую функцию.

Полученные в результате первичной обработки данные используются для решения задач математической статистики.