Диагонализируемые преобразования

Линейное преобразование называется диагонализируемым, если существует базис, в котором матрица линейного преобразования имеет диагональный вид. Заметим, что базис, в котором матрица линейного преобразования имеет диагональный вид, образован собственными векторами. Верно и обратное. В базисе из собственных векторов матрица линейного преобразования имеет диагональный вид. Не каждое линейное преобразование диагонализируемо. Например, линейное преобразование, заданное матрицей  не диагонализируемо.

Теорема 7.3. Собственные векторы, отвечающие различным собственным значениям, линейно независимы.

Доказательство. Пусть  - линейно независимая система собственных векторов, соответствующих собственному значению , где i =1,…, s. Покажем линейную независимость системы векторов 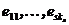 индукцией по s. При s =1 утверждение очевидно. Пусть оно верно для s -1. Покажем его справедливость для s. Допустим, система  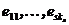- линейно зависима. Тогда найдутся коэффициенты  не все равные нулю, что . Из этого равенства выводим  или . По предположению индукции все коэффициенты в этом равенстве равны 0, и, значит  при i < s. Но тогда система  - линейно зависима, что противоречит условиям теоремы. К полученному противоречию привело допущение о линейной зависимости системы векторов 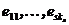, значит, эта система линейно независима, что и требовалось доказать.

Рассмотрим вопрос о количестве линейно независимых собственных векторов, соответствующих собственному числу .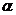

Геометрической кратностью собственного числа 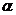 называется дефект преобразования 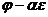, а алгебраической кратностью называется кратность корня  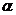в характеристическом многочлене.

Теорема 7.4. Геометрическая кратность 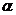 не превосходит его алгебраической кратности.

Доказательство. Пусть геометрическая кратность 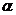 равна k. Дополним базис  ядра преобразования 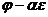 до базиса всего пространства . Матрица линейного преобразования в этом базисе имеет вид  и характеристический многочлен равен . Таким образом, алгебраическая кратность 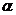 не меньше геометрической кратности, что и требовалось доказать.

Теорема 7.5 Линейное преобразование  линейного пространства V над числовым полем P диагонализируемо тогда и только тогда, когда характеристический многочлен раскладывается над полем P на линейные множители и алгебраическая кратность каждого корня совпадает с его геометрической кратностью.

Доказательство очевидно.

Теорема Шура

Пусть  - линейное преобразование пространства V над полем комплексных чисел C. Линейное преобразование  имеет хотя бы один собственный вектор (Следствие 7.1). Этот факт можно усилить.

Теорема 7.6. Пусть  - линейное преобразование пространства V над полем комплексных чисел C. Существует базис V, в котором матрица линейного преобразования  имеет верхний треугольный вид.

Доказательство проведем индукцией по размерности V. Пусть утверждение верно для линейных преобразований (n -1)-мерных пространств. Покажем его справедливость для линейного преобразования   n -мерного линейного пространства V. Поскольку линейное пространство над полем C, то существует собственный вектор h этого линейного преобразования. Дополним этот вектор до базиса всего пространства векторами 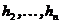. Матрица линейного преобразования в этом базисе имеет блочный вид , где 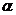 - собственное число для вектора h. Обозначим через W линейную оболочку векторов 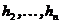. Векторы  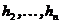образуют базис W. Обозначим через  линейное преобразование W, матрица которого в базисе 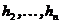 равна A. По предположению индукции в подпространстве W существует базис , в котором матрица линейного преобразования имеет верхний треугольный вид. Пусть T – матрица перехода к этому базису. Тогда 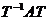 - верхняя треугольная матрица. Матрица перехода от базиса  к базису  равна , и, значит, матрица  в базисе  равна 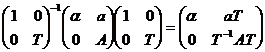, то есть является  верхней треугольной.

Аналогом доказанной теоремы над полем вещественных чисел является следующий результат.

Теорема 7.7. Пусть  - линейное преобразование пространства V над полем вещественных чисел R. Существует базис V, в котором матрица линейного преобразования  имеет блочный верхний треугольный вид. По главной диагонали стоят блоки первого и второго порядка.

Доказательство проведем индукцией по размерности n пространства V. Пусть утверждение верно для линейных преобразований пространств размерности меньшей n. Покажем его справедливость для линейного преобразования   n -мерного линейного пространства V. Линейное преобразование  имеет либо одномерное, либо двумерное инвариантное подпространство (Следствие 7.2). Дополним базис этого инвариантного подпространства до базиса всего пространства векторами , где k равно либо 2, либо 3. Матрица линейного преобразования в этом базисе имеет блочный вид , где 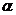 - блок либо первого, либо второго порядка. Далее, рассуждения повторяют доказательство теоремы 7.6.

Теорема 7.8. (теорема Шура). Для линейного преобразования  унитарного пространства V существует ортонормированный базис, в котором матрица линейного преобразования  имеет верхний треугольный вид.

Доказательство. Пусть 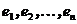 - базис V, в котором матрица линейного преобразования  имеет верхний треугольный вид (Теорема 7.6). Применим к базису процесс ортогонализации и построим ортогональный базис . Матрица перехода T от базиса 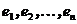 к базису  - верхняя треугольная и . Поскольку произведение верхних треугольных матриц является верхней треугольной матрицей, то матрица  - верхняя треугольная. Положим , где i = 1,…, n. Базис  - ортонормированный и матрица линейного преобразования в этом базисе – верхняя треугольная, тем самым теорема доказана.

Теорема 7.9. Для линейного преобразования  евклидова пространства V существует ортонормированный базис, в котором матрица линейного преобразования  имеет блочный верхний треугольный вид. По главной диагонали расположены блоки первого и второго порядков.

Доказательство аналогично доказательству теоремы 7.7.