Если вектор 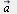 пространства имеет координаты пространства имеет координаты  , а вектор , а вектор  имеет координаты имеет координаты 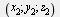 , то: , то:
| 
|
| Длина вектора в координатах в пространстве. | 
|
| Угол между двумя векторами в пространстве. | 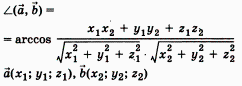
|
Условие коллинеарности векторов  в пространстве. в пространстве.
| 
|
Условие ортогональности векторов  в пространстве. в пространстве.
| 
|
Примеры решения задач:
Даны вектора  и
и 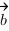

Найдите:
1. Сумму координат вектора 
2. Квадрат длины вектора 
3. Скалярное произведение векторов  и
и 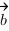
4. Угол между векторами  и
и 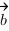
1. Найдем координаты векторов  и
и 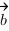 . Для этого сначала найдем координаты начала и конца каждого вектора:
. Для этого сначала найдем координаты начала и конца каждого вектора:

Чтобы найти координаты вектора, нужно из координат его конца вычесть координаты его начала:
Координаты вектора  .
.
Координаты вектора 
Координаты вектора  равны сумме соответствующих координат векторов
равны сумме соответствующих координат векторов  и
и 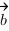 :
: 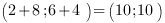
Сумма координат вектора  равна 20
равна 20
Ответ: 20.
2. Квадрат длины вектора равен сумме квадратов его координат, поэтому квадрат длины вектора  равен
равен 
Ответ: 200.
3. Скалярное произведение векторов  и
и  равно сумме произведений одноименных координат.
равно сумме произведений одноименных координат.

Ответ: 40.
4. Косинус угла  между векторами
между векторами 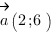 и
и  вычисляется по формуле:
вычисляется по формуле:

Отсюда 
Ответ: 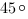
Упражнения для самостоятельной работы.
 1. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
1. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  .
.

 2. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
2. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  +
+ 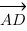 .
.

 3. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
3. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  -
- 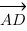 .(чертеж из предыдущей задачи).
.(чертеж из предыдущей задачи).
 4. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора
4. Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора  -
-  .
.
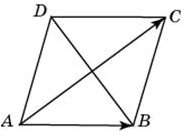
 5. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора
5. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  +
+ 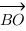 .
.

 6. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора
6. Диагонали ромба ABCD пересекаются в точке O и равны 12 и 16. Найдите длину вектора  –
– 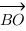 . (чертеж из предыдущей задачи).
. (чертеж из предыдущей задачи).
Список литературы
1. Геометрия, 10-11: Учеб. для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.-Москва: Просвещение, 2009 год
2. Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по геометрии для 10 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2007,- 175 с.
3. Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.сост.Г.И.Ковалёва, Н.И.Мазурова.- Волгоград: Учитель, 2009, 187 стр.
4. Виртуальная школа Кирилла и Мефодия. Репетитор по математике. Москва. 2007 год
5. Учебное электронное издание. Математика 5- 11 класссы. Практикум. Под редакцией Дубровского В.Н., 2004.
 Условные обозначения:
Условные обозначения:
Задания, которые необходимо выполнить на оценку «удовлетворительно»
 Дополнительные задания, которые необходимо выполнить на оценку «хорошо»
Дополнительные задания, которые необходимо выполнить на оценку «хорошо»
 Дополнительные задания, которые необходимо выполнить на оценку «отлично»
Дополнительные задания, которые необходимо выполнить на оценку «отлично»






