Многогранной поверхностью называют объединение конечного числа плоских многоугольников такое, что каждая сторона любого из многоугольников является в то же время стороной другого (но только одного) многоугольника, называемого смежным с первым многоугольником.
Виды многогранников:
Пирамида
Многогранни, одна из граней которого - произвольный многогранник, а остальные грани - треугольники, имеющие одну общую вершину, называется пирамидой.
Многоугольник называется основанием пирамиды, а остальные грани (треугольники) называются боковыми гранями пирамиды.
Различают треугольные, четырехугольные, пятиугольные и т.д. пирамиды в зависимости от вида многоугольника, лежащего в основании пирамиды.
Призма
Многогранник, две грани которого - равные n-угольники, лежащие в параллельных плоскостях, а остальные n граней - параллелограммы, называетсяn-угольной призмой.
многогранник пирамида призма параллелепипед
Пару равных n-угольников называют основаниями призмы. Остальные грани призмы называют ее боковыми гранями, а их объединение - боковой поверхностью призмы. На рис.1 изображена пятиугольная призма.
Стороны граней призмы называют ребрами, а концы ребер - вершинами призмы. Ребра, не принадлежащие основанию призмы, называют боковыми ребрами.
Призму, боковые ребра которой перпендикулярны плоскостям оснований, называют прямой призмой. В противном случае призма называется наклонной.
Отрезок перпендикуляра к плоскостям оснований призмы, концы которого принадлежат этим плоскостям, называют высотой призмы.
Прямая призма, основанием которой является правильный многоугольник, называется правильной призмой.
Параллелепипед
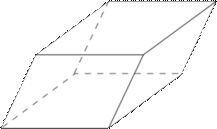
Параллелепипед - шестигранник, противоположные грани которого попарно параллельны. Параллелепипед имеет 8 вершин, 12 рёбер; его грани представляют собой попарно равные параллелограммы.
Параллелепипед называется прямым, если его боковые ребра перпендикулярны к плоскости основания (в этом случае 4 боковые грани - прямоугольники); прямоугольным, если этот параллелепипед прямой и основанием служит прямоугольник (следовательно, 6 граней - прямоугольники);
Параллелепипед, все грани которого квадраты, называется кубом.
Объём параллелепипеда равен произведению площади его основания на высоту.
Цилиндр
1. Цилиндр – тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов.
Цилиндр получается при вращении прямоугольника вокруг стороны.
2. прямая OO 
- ось цилиндра
отрезок OO - высота,
отрезок АА = ВВ - образующая
круг (О,ОВ) =кругу (O , O В ) – основание цилиндра
3. а) осевое сечение (проходит через ось) есть прямоугольник
б) сечение цилиндра плоскостью, параллельной его оси, представляет собой прямоугольник
в) сечение цилиндра плоскостью, перпендикулярной его оси, представляет собой круг
II. Конус
1. Конус – тело, которое состоит из круга – основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания.
Конус получается при вращении прямоугольного треугольника вокруг катета.
2. т. S – вершина конуса
круг(О,ОА) – основание конуса
SA=SB – образующие конуса
Отрезок SO – высота конуса
Прямая SO – ось конуса
3. а) осевое сечение конуса – равнобедренный треугольник
б) сечение конуса плоскостью, проходящей через его вершину – равнобедренный треугольник
в) сечение конуса плоскостью, перпендикулярно оси симметрии – круг
4. а) вписанная пирамида – пирамида, основание которой есть многоугольник, вписанный в окружность основания конуса, вершина – вершина конуса, боковые ребра пирамиды – образующие конуса
б) Касательной плоскостью к конусу называется плоскость, проходящая через образующую конуса и перпендикулярная плоскости осевого сечения, содержащей эту образующую.
Шар. Сфера
1. Шар – тело состоящее из всех точек пространства, находящихся на расстоянии не больше данного от данной точки.
Сфера – граница шара.
Шар получается при вращении полукруга вокруг его диаметра как оси
2. т. О – центр шара
ОА=ОВ – радиус шара
АВ – диаметр
3. а) Всякое сечение шара плоскостью – круг, центром которого является основание перпендикуляра, опущенного из центра шара на секущую плоскость.
б) плоскость, проходящая через центр шара – диаметральная плоскость. Сечение шара диаметральной плоскостью называется большим кругом, а сечение сферы – большой окружностью.
4. 
Плоскость проходящая через точку А поверхности шара и перпендикулярная радиусу, проведенному в точку А, называется касательной плоскостью, точка А – плоскостью касания.
а) многогранник называется вписанным в шар, если все его вершины лежат на поверхности шара.
б) многогранник называется описанным около шара, если все его грани касаются поверхности шара
Площади тел вращения
Площадь боковой поверхности цилиндра
Площадь полной поверхности цилиндра
| 
|
Площадь боковой поверхности конуса
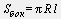Площадь полной поверхности конуса
| 
|
Площадь боковой поверхности усеченного конуса
Площадь полной поверхности усеченного конуса
| 
|
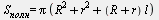
Примеры решения задач
1. В правильной шестиугольной пирамиде SABCDEF, стороны основания которой равны 1, а боковые ребра равны 2, найдите расстояние от точки А до плоскости SBC.
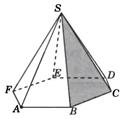
Решение. Пусть О – центр основания пирамиды. Прямая АО параллельна прямой ВС и, значит, параллельна плоскости SBC. Следовательно, искомое расстояние равно расстоянию от точки О до плоскости SBC. Пусть G – середина отрезка ВС. Тогда прямая ОG перпендикулярна ВС и искомым перпендикуляром, опущенным из точки О на плоскость SBC, является высота ОН прямоугольного треугольника SOG. В этом треугольнике
2. В единичном кубе А…D1 найдите угол между прямыми DА1 и ВD1.
Решение. АD1 является проекцией прямой ВD1 на плоскость АDD1. Прямые АD1 и DА1 перпендикулярны. Из теоремы о трех перпендикулярах следует, что прямые DА1 и ВD1 также перпендикулярны, т.е. искомый угол равен 900.
Упражнения для самостоятельной работы
Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).
1 вариант
2 вариант
Решить кроссворд
1 вариант
| 11 | ||||||||||||
| 1 | ||||||||||||
| 10 | ||||||||||||
| 2 | ||||||||||||
| З | ||||||||||||
| 3 | 4 | |||||||||||
| 9 | ||||||||||||
| 5 | ||||||||||||
| 6 |
1 в.
По горизонтали
1..Перпендикуляр, опущенный из вершины конуса на плоскость (высота)
2. Плоскость, проходящая через образующую цилиндра, параллельно осевому сечению (касательная)
3. Сечение цилиндра плоскостью, параллельной основанию (круг)
4. Сечение конуса плоскостью, параллельной основанию (круг)
5. Отрезок, соединяющий две точки шаровой поверхности и проходящей через центр шара (диаметр)
6. Тело, состоящее из всех точек пространства, находящихся на расстоянии, не большем данного (шар)
По вертикали
- Тело, состоящее из круга и точки, не лежащей в плоскости этого круга, и всех отрезков, соединяющих эту точку с точками круга. (конус)
- Отрезок, соединяющий вершину конуса с точками окружности основания (образующая)
- Граница шара (сфера)
- Сечение цилиндра плоскостью, проходящей через ось цилиндра (осевое)
- Тело, состоящее из двух кругов, совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (цилиндр)
2 вариант.
| 9 | |||||||||||||||
| 1 | |||||||||||||||
| 2 | |||||||||||||||
| 6 | |||||||||||||||
| 3 | |||||||||||||||
| 8 | |||||||||||||||
| 4 | |||||||||||||||
| 5 | |||||||||||||||
По горизонтали
1. Количество сходящихся ребер у октаэдра (четыре)
2. Грань додекаэдра (пятиугольник)
3. Боковая грань усеченной пирамиды (трапеция)
4. Правильный многогранник (октаэдр)
5. Сечение, проходящее через вершину пирамиды и диагональ основания (диагональное)
По вертикали
2. Граница многогранника (поверхность)
6. Правильная треугольная пирамида (тетраэдр)
7. Перпендикуляр, опущенный из вершины пирамиды на плоскость основания (высота)
8. Элемент пирамиды (грань)
9. Пирамида, у которой основание правильный многоугольник, а вершина проецируется в его центр (правильная)
Список литературы
Геометрия, 10-11: Учеб. для общеобразовательных учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С. Б. Кадомцев и др.-Москва: Просвещение, 2009 год
2. Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по геометрии для 10 класса.- 4-е издание, испр. и доп.- М.:Илекса, 2007,- 175 с.
3. Геометрия. 10-11 классы: тесты для текущего и обобщающего контроля/авт.сост.Г.И.Ковалёва, Н.И.Мазурова.- Волгоград: Учитель, 2009, 187 стр.
4. Виртуальная школа Кирилла и Мефодия. Репетитор по математике. Москва. 2007 год
5. Учебное электронное издание. Математика 5- 11 класссы. Практикум. Под редакцией Дубровского В.Н., 2004.
ПРАКТИЧЕСКАЯ РАБОТА № 15
« Измерения в геометрии »
Цель урока:
1) Обобщить теоретические знания по теме: «Измерения в геометрии».
2) Рассмотреть алгоритмы решений заданий теме «Измерения в геометрии», решить задачи.
3) Формировать умения прогнозировать собственную деятельность, умение организовать свою деятельность и анализировать ее.
Теоретический материал
