1. Письменная работа на листочках по проверке решения задач на построение циркулем и линейкой:
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
2. Проверить решение домашней задачи № 149 на доске.
Решение
Акцентируем внимание учащихся на том, что вначале необходимо начертить все фигуры, данные в условии задачи. В данной задаче чертим прямую а, отрезок РQ и отмечаем точку В так, что В  а. Далее проводим окружность радиуса PQ с центром в точке В. Пусть М – одна из точек пересечения этой окружности с прямой а. Точка М искомая, так как М
а. Далее проводим окружность радиуса PQ с центром в точке В. Пусть М – одна из точек пересечения этой окружности с прямой а. Точка М искомая, так как М 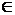 а и ВМ = РQ. Остается выяснить, всегда ли задача имеет решение. Ответ на этот вопрос учащиеся могут дать с помощью рисунка:
а и ВМ = РQ. Остается выяснить, всегда ли задача имеет решение. Ответ на этот вопрос учащиеся могут дать с помощью рисунка:

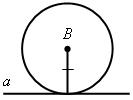

а б в
Указание: задача (в) не имеет решений.
II. Решение задач.
1. На доске и в тетрадях решить задачу № 152.
Решение
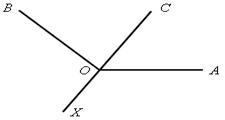
Начертим тупой угол АОВ, построим биссектрису ОС этого угла и проведем продолжение ОХ луча ОС. Луч ОХ искомый. Убедимся в этом. По построению ОС – биссектриса  АОВ, поэтому
АОВ, поэтому  АОС =
АОС =  СОВ =
СОВ =
= 
 АОВ и углы АОС и СОВ острые. По построению углы АОС и АОХ, а также углы СОВ и ВОХ смежные. Сумма смежных углов равна 180°, поэтому из равенства
АОВ и углы АОС и СОВ острые. По построению углы АОС и АОХ, а также углы СОВ и ВОХ смежные. Сумма смежных углов равна 180°, поэтому из равенства  АОС =
АОС =  ВОС следует, что
ВОС следует, что  АОХ =
АОХ =  ВОХ. Так как углы АОС и СОВ острые, то смежные с ними углы АОХ и ВОХ тупые.
ВОХ. Так как углы АОС и СОВ острые, то смежные с ними углы АОХ и ВОХ тупые.
2. Решить задачу № 165 на доске и в тетрадях.
Указание: первая часть решения задачи (пункта) не вызывает затруднений у учащихся.
Для доказательства того факта, что точка О лежит на прямой KK 1 (пункт б), надо рассмотреть луч ОK 2, являющийся продолжением луча ОK, и доказать, что лучи ОK 1 и ОK 2 совпадают. Тем самым будет доказано, что точки K, О и K 1 лежат на одной прямой.
III. Самостоятельная работа (10 минут).
Вариант I

| 1. На рисунке АВ = АС и  АСЕ = = АСЕ = =  АВD.
1) Докажите, что АВD.
1) Докажите, что 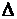 АСЕ = АСЕ = 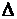 АВD.
2) Найдите сторонытреугольника АВD, если АЕ = 15 см, ЕС = 10 см, АС = 7 см. АВD.
2) Найдите сторонытреугольника АВD, если АЕ = 15 см, ЕС = 10 см, АС = 7 см.
|
2. Известно, что в треугольниках АВС и А 1 В 1 С 1  А =
А =  А 1, АВ = А 1 В 1, АС = А 1 С 1. На сторонах ВС и В 1 С 1 отмечены точки K и K 1 такие, что СK =
А 1, АВ = А 1 В 1, АС = А 1 С 1. На сторонах ВС и В 1 С 1 отмечены точки K и K 1 такие, что СK =
= С 1 K 1. Докажите, что 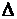 АВК =
АВК = 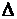 А 1 В 1 K 1.
А 1 В 1 K 1.
Вариант II
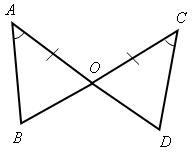
| 1. На рисунке АО = СО и  ВАО = = ВАО = =  DСО.
1) Докажите, что DСО.
1) Докажите, что 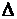 АОВ = АОВ = 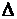 СОD.
2) Найдите углы СОD.
2) Найдите углы 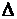 АОВ, если АОВ, если  ОСD = 37°, ОСD = 37°,  ОDС = 63°, ОDС = 63°,  СОD = 80°. СОD = 80°.
|
2. Известно, что в треугольниках АВС и А 1 В 1 С 1  В =
В =  В 1, АВ = А 1 В 1и ВС = В 1 С 1.На сторонах АС и А 1 С 1отмечены точки D и D 1так, что АD =
В 1, АВ = А 1 В 1и ВС = В 1 С 1.На сторонах АС и А 1 С 1отмечены точки D и D 1так, что АD =
= А 1 D 1.Докажите, что 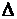 ВDС =
ВDС = 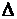 В 1 D 1 С 1.
В 1 D 1 С 1.
IV. Итоги урока.
Домашнее задание: подготовиться к устному опросу по карточкам, повторив материал пунктов 15–20; решить задачи №№ 158, 166.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Вариант I
1) Отложить от данного луча угол, равный данному.
2) Построить середину данного отрезка.
Вариант II
1) Построить биссектрису данного неразвернутого угла.
2) Построить прямую, проходящую через данную точку и перпендикулярную к прямой, на которой лежит данная точка.
Урок 19
РЕШЕНИЕ ЗАДАЧ. ПОДГОТОВКА К КОНТРОЛЬНОЙ РАБОТЕ.
Цели: закрепить навыки в решении задач на применение признаков равенства треугольников; проверить знания учащихся; подготовить учащихся к предстоящей контрольной работе.
Ход урока






