1. Определение равнобедренного треугольника; его боковые стороны и основание (рис. 63).
2. Определение равностороннего треугольника.
3. Устно решить задачи (по готовым чертежам):
1) Дан равнобедренный треугольник СDЕ с основанием DЕ. Назовите боковые стороны, углы при основании и угол, противолежащий основанию этого треугольника.
2) В равнобедренном треугольнике МDK МK = DK. Назовите боковые стороны, основание, угол, противолежащий основанию, и углы при основании этого треугольника.
4. Доказательство теоремы о свойствах углов при основании равнобедренного треугольника.
Чертеж, краткую запись условия и заключение теоремы, а также основные этапы доказательства полезно записать на доске и в тетрадях учащихся.
Дано:  АВС – равнобедренный, ВС – основание.
АВС – равнобедренный, ВС – основание.
Доказать:  В =
В =  С.
С.
Доказательство
Проведем биссектрису АD треугольника (рис. 64 учебника).  АВD =
АВD =
=  АСD по двум сторонам и углу между ними (АВ = АС по условию,
АСD по двум сторонам и углу между ними (АВ = АС по условию,
АD – общая сторона,  1 =
1 =  2, так как АD – биссектриса).
2, так как АD – биссектриса).
Значит,  В =
В =  С, что и требовалось доказать.
С, что и требовалось доказать.
Это свойство в дальнейшем часто используется при решении задач и доказательстве теорем, поэтому оно должно быть хорошо усвоено.
III. Закрепление изученного материала.
1. Решить задачу № 108.
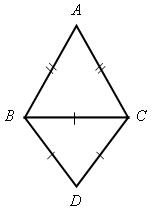
| Дано: 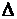 АВС – равнобедренный; АВС – равнобедренный;
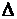 ВСD – равносторонний.
Р D АВС = 40 см; Р D ВСD = 45 см.
Найти: АВ и ВС.
Решение
ВС = СD = ВD (по условию),
Р D ВСD = 45 см = 3 ВС, отсюда
ВС = 45: 3 = 15 (см).
По условию Р D АВС = 40 см, ВС = 15 см, тогда АВ + АС = 40 – 15 = 25 (см). ВСD – равносторонний.
Р D АВС = 40 см; Р D ВСD = 45 см.
Найти: АВ и ВС.
Решение
ВС = СD = ВD (по условию),
Р D ВСD = 45 см = 3 ВС, отсюда
ВС = 45: 3 = 15 (см).
По условию Р D АВС = 40 см, ВС = 15 см, тогда АВ + АС = 40 – 15 = 25 (см).
|
Так, по условию 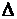 АВС – равнобедренный, то АВ = АС = 25: 2 =
АВС – равнобедренный, то АВ = АС = 25: 2 =
= 12,5 (см).
Ответ: АВ = 12,5 см; ВС = 15 см.
2. Устно решить задачу № 116.
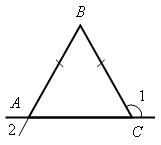
3. Задачу № 112 по рисунку 66 решить на доске и в тетрадях.
Дано: 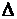 АВС; АВ = ВС;
АВС; АВ = ВС;  1 = 130°.
1 = 130°.
Найти:  2.
2.
| Решение
По условию АВ = ВС, тогда  АВС – равнобедренный по определению, значит, АВС – равнобедренный по определению, значит,  ВАС = ВАС =  ВСА (по свойству равнобедренного треугольника). ВСА (по свойству равнобедренного треугольника).  ВСА + ВСА +  1 = 180° (свойство смежных углов).
Отсюда 1 = 180° (свойство смежных углов).
Отсюда  ВСА = 180° – ВСА = 180° –  1 = 180° – – 130° = 50°; значит, и 1 = 180° – – 130° = 50°; значит, и  ВАС = 50°. ВАС = 50°.
|
Так как  ВАС =
ВАС =  2 (вертикальные углы равны), то
2 (вертикальные углы равны), то  2 = 50°.
2 = 50°.
Ответ: 50°.
4. Разобрать решение задачи сначала устно путем логических рассуждений, строя чертежи, а затем решение записать на доске и в тетрадях.
В равнобедренном треугольнике сумма всех углов равна 180°. Найдите углы этого треугольника, если известно, что:
а) один из них равен 105°;
б) один из них равен 38° (рассмотреть два случая).
IV. Итоги урока.
Домашнее задание: изучить п. 18 с доказательством теоремы об углах при основании равнобедренного треугольника; ответить на вопросы 10–12 на с. 50; решить задачи №№ 104, 107 и 117.
Урок 17
РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «РАВНОБЕДРЕННЫЙ ТРЕУГОЛЬНИК»
Цели: изучить свойство биссектрисы (медианы, высоты) равнобедренного треугольника, проведенной к основанию; изучить признак равнобедренного треугольника и закрепить знание свойств равнобедренного треугольника при решении задач; развивать логическое мышление учащихся.
Ход урока






