Число тогда и только тогда делится на 2, когда оно оканчивается четной цифрой.
Число тогда и только тогда делится на 5, когда оно оканчивается цифрой 0 или цифрой 5.
Доказательство. Любое число S в десятичной системе счисления представимо в виде:
S = аn ·10 n + аn -1 · 10 n -1+... + а 1 · 10 + а0.
Очевидно, все слагаемые, кроме последнего, делятся на 2 и на 5, ведь 10 
2 и 0 5.
Что можно сказать о числе S? Делится ли оно на 2 и на 5? Все зависит от а 0 (от последней цифры). a 0 2 Þ S 2, а 0 5 Þ S 5(свойство о делимости суммы на число). Обратно, S 2 Þ а 0 2, S 5 Þ а 0 5(свойство о делимости разности на число).
Значит, S 2 Û а 0 2; S 5 Û а 0 5.
Все аi – цифры, 0 ≤ аi £ 9. То есть на 2 будут делиться числа, оканчивающиеся на 0, 2, 4, 6, 8, а на 5 числа, оканчивающиеся на 0, 5. И только такие числа.
Признаки делимости на 2 и 5 не случайно одинаковы. 2 и 5 – это делители числа 10 – основания десятичной системы счисления.
Признаки делимости на 4 и 25.
Число тогда и только тогда делится на 4, когда две его последние цифры образуют число, делящееся на 4.
Число тогда и только тогда делится на 25, когда две его последние цифры образуют число, делящееся на 25, т.е. 00, 25, 50, 75.
Доказательство. Заметим, что числа 4 и 25 делители числа 100. Пусть S любое натуральное число, в десятичной системе счисления его можно представить так:
S = ап · 10 n + аn- 1 · 10 n -1 +... + а 2 × 102 + а 1 · 10 + а 0.
Все слагаемые, кроме последних двух, содержат множителем число 100, а потому они делятся на 4 и 25.
Делится ли S на 4 и на 25 зависит от суммы слагаемых а 1 · 10 + а 0,т.е. от числа, образованного последними двумя цифрами. Для того, чтобы S делилось на 4, достаточно чтобы а 1 · 10+ а 0делилось на 4. Обратное утверждение тоже верно.
Для того, чтобы S делилось на 25, достаточно чтобы а 1 · 10 + а 0делилось на 25, т.е. чтобы S оканчивалось на 00, 25, 50, 75. Обратное утверждение тоже верно.
Значит, S 4 Û (а 1 · 10 + а 0) 4; S 25 Û (а 1 · 10 + а 0) 25.
Выведем теперь признаки делимости на 3 и 9.
Число тогда и только тогда делится на 3, когда сумма его цифр делится на 3.
Число тогда и только тогда делится на 9, когда сумма его цифр делится на 9.
Доказательство. Пусть S – любое натуральное число. Представим его так:
S = an · 10 n + an -1· 10 n- 1 + … + a1 · 10 + a0, где an, an -1, …, a 1, a 0 – цифры.
Перепишем число S так:
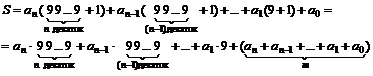
Очевидно, что число, записанное одними девятками, делится на 9. Т.е. все слагаемые, кроме последнего т = аn + аn -1+... + а2 + а1 + а0, делятся на 9 (по делимости суммы на число). Если т 9, то S 9.
Обратно, из S 9 Þ m 9(по делимости разности на число).
Значит, S 9 Û (аn + аn -1+... + а 2+ а 1 + а 0) 9.
Признак делимости на 3 доказывается точно также, ибо любое число, записанное одними девятками, делится на 3.
Признаки делимости на 3 и 9 одинаковы не случайно, 3 и 9 – делители числа 10 – 1, т.е. числа на 1 меньшего основания десятичной системы счисления. Заметим, что признак делимости на 3 и 9 зависит от суммы цифр числа.
