План:
§ 1. Определение алгоритма
§ 2. Формальное исполнение алгоритма
§ 3. Команда ветвления.
§ 4. Команда повторения
Алгоритмы встречаются в науке на каждом шагу: умение решать задачу «в общем виде», всегда означает, по существу, владение некоторым алгоритмом.
Слово алгоритм происходит от латинской формы написания имени великого математика IX века аль-Хорезми, который сформулировал правила выполнения арифметических действий.
Однако, строгое математическое определение термина «алгоритм» удалось сформулировать сравнительно недавно российским ученым А.Н. Колмогорову (1903-1987) и А.А. Маркову (1903–1979).
В последнее время вопросы, связанные с теорией алгоритмов, выросли в большую «теорию алгоритмов», потребность в которой вызвана появлением компьютеров.
Нами будет дана формулировка, лишь описывающая это понятие, и перечислены свойства, позволяющие определить, является ли конкретное предписание алгоритмом или нет.
Определение алгоритма
Любой человек ежедневно встречается с множеством задач от самых простых и хорошо известных до очень сложных. Для многих задач существуют определенные правила (инструкции, предписания), объясняющие исполнителю, как решить данную задачу.
Эти правила человек может изучить заранее или сформулировать сам в процессе решения задачи. Чем точнее и понятнее будут описаны правила решения задач, тем быстрее человек овладеет ими и будет эффективнее их применять.
Решение многих задач человек может передавать техническим устройствам – автоматам, ЭВМ, роботам. Применение таких технических устройств предъявляет очень строгие требования к точности описания правил и последовательности их выполнения. Поэтому разрабатываются специальные языки для четкого и строгого описания различных правил.
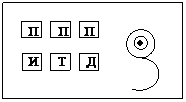
Допустим, вам нужно объяснить товарищу, как проехать к вам домой. Это может выглядеть следующим образом: «Выйти из института, дойти до остановки троллейбуса «ул. Мира», сесть в троллейбус № 2 (или № 13), проехать до остановки «Технологический техникум», выйти из троллейбуса, перейти улицу и в доме № 30 найти квартиру № 6». Итак, прозвучал алгоритм движения к дому. Новому понятию, приведенному в примере, следует дать определение, оно изображено в виде дорожки, которую мы выложили своему другу на пути к дому (рис. 1).
Рис. 1 | На плиточках написаны первые буквы ключевых слов определения: алгоритм это есть Предписание исполнителю, в котором Понятно и Точно описана Последовательность Действий, ведущих к достижению поставленной Цели или решению Задачи. |
В конце дорожки расположена мишень, символизирующая цель, и буква З – задача.
Дорожка – это алгоритм (а если говорить строго, его художественный образ). Какими же свойствами он должен обладать, чтобы привести нас к цели или к решению задачи? Обратимся вновь к нашему примеру. Что нужно, чтобы прийти в дом? Очевидно, в первую очередь, нужен сам ДОМ – с этих букв начинаются названия трех фундаментальных свойств алгоритма:
Д искретность, О пределенность, М ассовость.
Однако ДОМ – это еще не все, что нужно, чтобы прийти в него. Нужно еще пройти через КПП (контрольно-пропускной пункт). В нашем случае это еще три свойства алгоритма. Эти свойства – К онечность, П онятность, П равильность.
Первоначально под алгоритмами понимали только правила выполнения четырех арифметических действий над многозначными числами. В дальнейшем это понятие стали использовать вообще для обозначения последовательности действий, приводящих к решению задачи.
В качестве примеров алгоритмов математического характера можно привести правила выполнения арифметических действий над многозначными числами («столбиком»), правила выполнения таких же операций над дробями, описания решений различных задач на построение в геометрии.
Приведем пример. Вычислить значения У по формуле У = (АХ + В) (СХ – D) для любого значения X. Чтобы решить эту задачу, достаточно выполнить последовательность следующих действий:
1) умножить А на X, результат обозначить R 1;
2) R 1 сложить с В, результат обозначить R 2;
3) умножить С на X, результат обозначить R 3;
4) из R 3 вычесть D результат обозначить R 4;
5) умножить R 2 на R 4, считать результат значением У.
Это предписание является алгоритмом решения поставленной задачи. Для человека, выполняющего действия, уже не обязательно знать исходную формулу для вычисления значения У. Ему нужно всего лишь строго следовать указанному предписанию, исполняя его пункт за пунктом.
Этот пример показывает, что запись алгоритма распадается на отдельные указания исполнителю выполнить некоторое законченное действие. Каждое такое указание называется командой. Команды алгоритма выполняются одна за другой. На каждом шаге исполнения алгоритма исполнителю точно известно, какая команда должна выполняться следующей. Поочередное выполнение команд алгоритма за конечное число шагов приводит к решению задачи, к достижению цели.
Каждый алгоритм строится в расчете на некоторого исполнителя, который в состоянии выполнить каждое действие, предписываемое командами алгоритма. Совокупность команд, которые могут быть выполнены исполнителем, называется системой команд исполнителя.
Алгоритм должен быть понятным исполнителю, т.е. каждая его команда должна входить в систему команд исполнителя. Таким образом, для правильного построения алгоритма необходимо знать систему команд исполнителя и быть уверенным, что исполнение алгоритма всегда завершится за конечное число шагов.
Способы представления алгоритма:
1) устная форма;
2) письменная форма;
3) формула;
4) таблица;
5) программа (например, клавиши для микрокалькулятора);
6) графический способ – блок-схема (при составлении программы для ЭВМ). Блоки изображаются в виде геометрических фигур, соединяются между собой и нумеруются;
7) программы для ЭВМ.