Говоря «математическое доказательство», мы имеем в виду доказательство математического предложения. Доказательства, по способу ведения, подразделяются на прямые и косвенные.
Прямым доказательством теоремы Т называется конечная последовательность предложений j 1, j 2,..., j n данной теории, удовлетворяющая следующим требованиям:
1) предложение j 1 – какое-либо несомненное начало;
2) каждое предложение j i последовательности или аксиома, или получается из предшествующих предложений по какому-либо из правил вывода математической логики;
3) последнее предложение последовательности j n есть Т.
Ввиду того, что в соответствии с этим определением формальные доказательства являются очень длинными (состоят из большого числа предложений), их сокращают, допуская в качестве посылок наряду с аксиомами ранее доказанные теоремы и определения.
Доказательство называется косвенным (непрямым), если истинность теоремы обосновывается посредством опровержения истинности противоречащей теоремы. Например, в математике часто используют различные варианты косвенного доказательства (известного из школьного курса под названием доказательства способом «от противного»).
Косвенное доказательство некоторой теоремы Т состоит в том, что исходят из отрицания Т и выводят из него ложное заключение. Это выведение называют «приведением к нелепости», или «приведением к абсурду». Основная форма косвенного доказательства начинается с  и оканчивается предложением типа
и оканчивается предложением типа 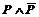 . В завершение такого доказательства обычно говорят: «полученное противоречие доказывает теорему».
. В завершение такого доказательства обычно говорят: «полученное противоречие доказывает теорему».
Среди косвенных доказательств встречаются разделительные, в которых есть разделительное суждение вида «S есть Р 1, Р 2», где число всевозможных случаев n ³ 2 и конечно.
По форме умозаключения, в которой совершаются доказательства, различают индуктивные и дедуктивные. Индуктивные доказательства получаются в результате применения методов полной индукции и математической индукции.
Метод математической индукции – специальный метод доказательства, применяющийся к предложениям типа (" n Î N) P (n), т.е. к предложениям, выражающим некоторое свойство Р, присущее любому натуральному числу n. Многие утверждения содержат целочисленную переменную n, и если надо доказать, что утверждение верно для любого числа n ³ n 0, то это можно осуществить в два этапа:
1) Утверждение проверяют для n = n 0.
2) Предположив, что утверждение справедливо для некоторого n = k ³ n 0, доказывают его праведливость для n = k + 1.
Если это осуществлено, то утверждение оказывается (этап 1) верным для n = n 0 и следовательно (этап 2), для n = n 0 + 1. Тогда (этап 2) оно верно для n = n 0 + 2 и т.д.
Эти этапы составляют основу метода математической индукции.
П р и м е р. Докажем методом математической индукции, что для всех n ³ 1 верное равенство
 .
.
Для упрощения выкладок введем обозначение S (n) = 1 + 2 + … + n; требуется доказать, что для всех n ³ 1 верно равенство 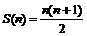 .
.
1) Для n = 1 оно очевидно.
2) Допустим, что для n = k оно выполнено, т.е. 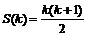 . Докажем, что тогда исходное равенство верно и для n = k + 1, т.е.
. Докажем, что тогда исходное равенство верно и для n = k + 1, т.е. 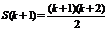 . Действительно, S (k + 1) = 1 + 2 + … + k + (k + 1) =
. Действительно, S (k + 1) = 1 + 2 + … + k + (k + 1) =
= 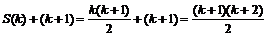 .
.
Ввиду того, что непосредственная проверка наличия этого свойства у любого натурального числа невозможна из-за бесконечности множества N, поступают так: устанавливают наличие этого свойства для n = 1 и доказывают, что из допущения о наличии его для n = k, где k – произвольное натуральное число, следует наличие этого свойства и для n = k + 1, т.е. для числа, «непосредственно следующего за k».
После этого заключают об истинности предложения (" n Î N) P (n), т.е. о том, что свойством Р обладает любое натуральное число.
Нестрогое гипотетическое обоснование суждений, основанное на применении одних только умозаключений правдоподобия (вероятности), например, неполной индукции или аналогии, не является доказательством. Подавляющее большинство математических предложений доказывается на основе дедуктивных умозаключений – умозаключений достоверности. Математические доказательства – это в основном чисто дедуктивные доказательства. Они представляют собой цепочки дедуктивных силлогизмов.
Правильные умозаключения
Умозаключение – это форма мышления или логическое действие, в результате которого из одного или нескольких известных нам определенным образом связанных суждений получается новое суждение, в котором содержится новое значение.
Форма записи умозаключения такова:  . Над чертой записаны Р 1, Р 2 ,..., Рn – исходные высказывания, они называются посылками. Под чертой записано высказывание Р, которое логически следует из исходных и называется заключением или выводом.
. Над чертой записаны Р 1, Р 2 ,..., Рn – исходные высказывания, они называются посылками. Под чертой записано высказывание Р, которое логически следует из исходных и называется заключением или выводом.
Заключение следует из посылок либо по правилам формальной логики (является простым логическим следствием посылок), либо выводится по правилам математики и формальной логики.
Умозаключения, позволяющие строить из общих суждений частные, называются дедуктивными или дедукцией.
Схема такого рассуждения записывается так: 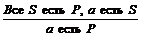
и называется правилом заключения.
П р и м е р. Если четырехугольник – параллелограмм, то его диагонали пересекаясь делятся пополам. АВСD – параллелограмм. Следовательно, его диагонали пересекаясь, делятся пополам.
Существуют еще два вида дедуктивных умозаключений. Приведем их схемы.
1) 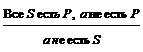 – правило отрицания.
– правило отрицания.
П р и м е р. В любом прямоугольнике противоположные стороны попарно равны. В четырехугольнике АВСD противоположные стороны попарно не равны, значит, АВСD – не прямоугольник.
2)  – правило силлогизма.
– правило силлогизма.
П р и м е р. Если числитель меньше знаменателя, то дробь правильная. Если дробь правильная, то она меньше 1. Следовательно, если числитель дроби меньше знаменателя, то дробь меньше 1.
Умозаключение, в результате которого на основании знания об отдельных предметах данного множества получается общий вывод, называется индуктивным или полной индукцией.
Его схема выглядит следующим образом:

П р и м е р. При умножении любого натурального числа на 5 последняя цифра в записи произведения 0 или 5.
Если натуральное число оканчивается на 0, то произведение оканчивается нулем. Если натуральное число оканчивается на 1, то произведение оканчивается на 5 и т.д. до 9. Переберем все возможные случаи. Значит, при умножении любого натурального числа на 5 последняя цифра в записи произведения 0 или 5.
Вопросы и задания для самопроверки
1. Установите способы определения следующих понятий из начального курса математики: математическое выражение, однозначное число, двузначное число, нечетное число, деление, произведение, сантиметр.
2. Докажите с помощью таблицы истинности равносильности:
(A Ú B) Ù C Û (A Ù C) Ú (B Ù C);
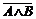 Û
Û 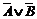 ;
;
 Û
Û 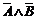 .
.
3. Можно ли установить значение истинности следующих высказываний, приводя конкретные примеры: а) от перестановки слагаемых сумма не изменяется; б) некоторые натуральные числа являются решениями неравенства х + 5 < 0.
Для высказывания б) постройте отрицание двумя различными способами.
3. Приведите примеры умозаключений, построенных по правилам отрицания и силлогизма.






