ВЫЧИСЛИТЕ базисные и цепные индексы цен (общие) с постоянными и переменными весами по этим продуктам.
Примечание. При вычислении индексов с постоянными весами примите за веса объем реализованных товаров в январе.
ЗАДАЧА 170
По шоколадной фабрике известны следующие данные:
| Изделие | Произведено по годам, кг | Неизменные цены за 1 кг, ден. ед. | ||
| Конфеты | 3,5 | |||
| Шоколад | 10,0 |
Вычислите цепные и базисные индексы физического объема продукции по шоколадной фабрике в целом. Сделайте выводы.
ЗАДАЧА 171
Трудоемкость единицы продукции в базисном и текущем периодах составила соответственно 0,25 и 0,20 ч. ОПРЕДЕЛИТЕ индивидуальные индексы трудоемкости продукции и средней часовой выработки.
ЗАДАЧА 172
На сколько процентов снизилась трудоемкость продукции, если выработка продукции в единицу времени увеличилась на 25%?
ЗАДАЧА 173
Стоимость произведенной предприятием продукции в сопоставимых ценах возросла на 6,2%, а производительность труда повысилась на 2,8%. КАК изменились общие затраты труда на предприятии?
ЗАДАЧА 174
Производительность труда на предприятии в текущем периоде по сравнению с базисным повысилась на 5,0%, при этом численность рабочих увеличилась на 36 человек и составила 472 человека. Как изменился физический объем продукции?
ЗАДАЧА 175
Как изменилась производительность труда на предприятии, если при том же объеме произведенной продукции общие затраты труда снизились на 15%.
ЗАДАЧА 176
Имеются следующие данные о трудоемкости продукции предприятия и объемах ее производства:
| Вид продукции | 1999 г. | 2000 г. | |||||
| Произведено, тыс. шт. | Затраты на 100 изделий, чел.-ч | Произведено тыс. шт. | Затраты на 100 изделий, чел.-ч | ||||
| А | |||||||
| Б | |||||||
ОПРЕДЕЛИТЕ общие индексы трудоемкости продукции, производительности труда и затрат труда. ПОКАЖИТЕ взаимосвязи между вычисленными индексами.
ЗАДАЧА 177
Известны следующие данные по предприятию за отчетный период:
| Изделие | Затраты рабочего времени на единицу продукции (чел.-ч) в периоде | Произведено продукции (шт.) в периоде | ||
| базисном | текущем | базисном | текущем | |
| 1-е | 5,0 | 4,5 | ||
| 2-е | 3,0 | 2,8 |
Вычислите общие индексы производительности труда, совокупных затрат рабочего времени и физического объема продукции (взвешенного по трудоемкости базисного периода).
ЗАДАЧА 178
Трудовые затраты и производительность труда на мебельной сборке характеризуется следующими данными:
| Вид мебели | Общие затраты времени, тыс. чел.-ч | Изменение производительности труда, % | |
| в 1-м квартале | во 2-м квартале | ||
| Мягкая | 38,4 | 38,0 | – 21,6 |
| Кухонная | 28,6 | 27,8 | +14,8 |
ОПРЕДЕЛИТЕ:
1) индивидуальные индексы производительности труда и физического объема продукции по каждому виду мебели;
2) общие индексы производительности труда и физического объема продукции.
ЗАДАЧА 179
Имеются следующие данные по швейной фабрике:
| Изделия | Фактические затраты рабочего времени в текущем периоде, тыс. чел.-ч | Индексы производительности труда, % |
| Дамские платья Мужские сорочки | 689,2 387,1 | 108,1 105,3 |
ВЫЧИСЛИТЕ общий индекс часовой производительности труда по фабрике.
ЗАДАЧА 180
Имеются следующие данные о ценах и реализации картофеля на колхозных рынках города:
| Рынок | Цена 1 кг, ден. ед. | Реализовано, т | ||
| в июле | в августе | в июле | в августе | |
| 1-й 2-й | 4,8 4,4 | 5,6 4,0 | 3,0 6,0 | 2,5 8,4 |
ОПРЕДЕЛИТЕ:
1) индексы цен по каждому рынку;
2) по двум рынкам вместе: а) индекс средних цен переменного состава; б) индекс цен постоянного состава; в) индекс влияния структурных сдвигов.
ПОЯСНИТЕ экономический смысл рассчитанных индексов.
ЗАДАЧА 181
Продажа яблок на двух рынках города характеризуется следующими данными:
| Рынок | Продажа яблок, тыс. кг | Средняя цена 1 кг, ден.ед. | ||
| в августе | в сентябре | в августе | в сентябре | |
| А | 1,0 | 1,5 | ||
| Б | 1,2 | 2,0 |
ОПРЕДЕЛИТЕ:
1) индексы цен по каждому рынку;
2) по двум рынкам вместе: а) индекс цен переменного состава; б) индекс цен постоянного состава; в) индекс влияния структурных сдвигов.
Сделайте выводы.
ЗАДАЧА 182
Себестоимость и объем производства однородной продукции по двум предприятиям характеризуются следующими данными:
| Предприятия | Себестоимость единицы изделия (ден. ед.) в периоде | Произведено изделий (тыс. шт.) в периоде | ||
| базисном | отчетном | базисном | отчетном | |
| 1,2 1,1 | 1,4 1,0 | 3,0 6,0 | 3,2 6,4 |
ОПРЕДЕЛИТЕ:
1) индексы себестоимости по каждому предприятию;
2) по двум предприятиям вместе: а) индекс средней себестоимости переменного состава; б) индекс себестоимости постоянного состава; в) индекс влияния структурных сдвигов.
ПОЯСНИТЕ полученные результаты.
ЗАДАЧА 183
Имеются следующие данные о производстве и себестоимости одноименной продукции по двум предприятиям:
| Предприятия | Базисный период | Текущий период | ||
| Произведено единиц | Себестоимость единицы, ден. ед. | Произведено единиц | Себестоимость единицы, ден. ед. | |
ОПРЕДЕЛИТЕ:
1) изменение себестоимости продукции на каждом предприятии;
2) индексы себестоимости продукции по двум предприятиям вместе: а) переменного состава; б) постоянного состава; в) индекс влияния структурных сдвигов в производстве продукции на изменение средней себестоимости продукции.
ЗАДАЧА 184
Объем производства и себестоимость одного и того же вида продукции по двум предприятиям представлены в таблице:
| Предприятия | Произведено продукции (тыс. шт.) в периоде | Себестоимость тысячи штук (ден. ед.) в периоде | ||
| базисном | отчетном | базисном | отчетном | |
| 70,0 | 80,0 | 18,0 | 24,0 | |
| 50,5 | 85,0 | 20,0 | 30,0 |
Вычислите индексы себестоимости переменного и постоянного состава и индекс влияния структурных сдвигов на изменение средней себестоимости. Сделайте выводы.
ЗАДАЧА 185
Имеются следующие данные об урожайности и размерах посевных площадей зерновых культур по двум сельскохозяйственным предприятиям:
| Сельскохозяйственные предприятия | Урожайность зерновых культур (ц/га) в периоде | Посевная площадь (га) в периоде | ||
| базисном | текущем | базисном | текущем | |
| 18,5 | 20,2 | |||
| 25,3 | 27,4 |
ОПРЕДЕЛИТЕ:
1) индексы урожайности по каждому сельскохозяйственному предприятию;
2) по двум сельскохозяйственным предприятиям вместе: а) индекс урожайности переменного состава; б) индекс урожайности постоянного состава; в) индекс влияния сдвигов в структуре посевных площадей на изменение средней урожайности.
Поясните полученные результаты.
ЗАДАЧА 186
На основании данных об урожайности зерновых культур и структуре посевных площадей, занятых зерновыми, по двум совхозам вычислите индексы урожайности переменного состава, постоянного состава и индекс влияния сдвигов в структуре посевных площадей на изменение средней урожайности:
| Сельскохозяйственное предприятие | Урожайность зерновых (ц/га) в периоде | Удельный вес посевной площади (в % к итогу) в периоде | ||
| базисном | отчетном | базисном | отчетном | |
| 18,2 | 19,8 | 60,0 | 40,0 | |
| 20,2 | 22,0 | 40,0 | 60,0 |
ЗАДАЧА 187
По изделию А имеются следующие данные о дневной выработке одного рабочего и отработанных человеко-днях по двум участкам цеха за 1 полугодие 1999 г.:
| Участок | Дневная выработка, шт. | Отработано, чел.-дней | ||
| в 1-м квартале | во 2-м квартале | в 1-м квартале | во 2-м квартале | |
ОПРЕДЕЛИТЕ индексы средней дневной выработки:
1) по каждому участку;
3) по двум участкам вместе: а) индекс средней дневной выработки переменного состава; б) индекс средней дневной выработки постоянного состава; в) индекс влияния изменения структуры отработанного времени на изменение средней выработки.
ПОЯСНИТЕ экономический смысл рассчитанных индексов.
ЗАДАЧА 188
Уровень рыночных цен на молочные продукты и объем их реализации в двух регионах характеризуются следующими данными:
| Продукт | Регион А | Регион Б | ||
| Цена за 1 кг, ден.ед. | Продано, т | Цена за 1 кг, ден.ед. | Продано, т | |
| Масло | ||||
| Сыр |
ОПРЕДЕЛИТЕ территориальный индекс цен региона А по отношению к региону Б, используя в качестве весов: а) объемы проданных товаров региона А; б) объемы проданных товаров региона Б; в) объемы проданных товаров по двум регионам, вместе взятым.
ЗАДАЧА 189
Себестоимость продукции, выпускаемой на двух предприятиях отрасли, и объемы ее производства характеризуются следующими данными:
| Вид продукции | Предприятие А | Предприятие Б | ||
| Себестоимость, ден.ед. | Произведено, шт. | Себестоимость, ден.ед. | Произведено, шт. | |
На основе суммарных объемов производства рассчитайте индекс себестоимости продукции предприятия А по сравнению с предприятием Б.
Тема 7. ИНТЕГРАЛЬНЫЕ МЕТОДЫ ФАКТОРНОГО АНАЛИЗА
Формула интегрального разложения абсолютного прироста результативного показателя по факторам, учитывающая любые закономерности развития явлений в случае исходной модели ∑Q=∑WT, выражающей зависимость суммарного объема товарной продукции структурных подразделений некоторого производственного формирования (∑Q) от изменения уровня производительности труда (W) и затрат рабочего времени (Т), имеет следующий вид:
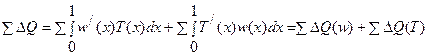, (7.1)
где х – аргумент функции (время); 0,1 – пределы интегрирования;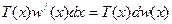 
– прирост результативного показателя ∑Q за счет фактора w на бесконечно малом интервале dx. То есть первый интеграл правой части равенства (7.1) характеризует прирост результативного показателя за весь период [0,1] по фактору w, а второй – по фактору Т.
При одновременном изменении факторов равенство (7.1) принимает следующий вид:
а) в предположении линейных тенденций развития факторов
∑∆Q=∑∆w(∆T/2 +T0)+∑∆T(∆w/2 +w0), (7.2)
где ∆Q(T)=∆T(∆w/2+w0), ∆Q(w)=∆w(∆T/2 +T0);
б) в предположении, что закономерности развития факторов характеризуются показательными функциями, -
∆Q(T)=К ln(T1/T0), ∆Q(w)=К ln(w1/w0), (7.3)
где К=∆Q/ln(Q1/Q0), если ∆Q≠0, или К=Q0 если ∆Q=0.
В случае применения формул (7.2) и (7.3) для расчета факторных оценок по частям периода [0,1] итоговые факторные оценки за весь период в целом будут равны суммам соответствующих частных факторных оценок.
Формула интегрального разложения полного индекса результативного показателя по факторам, учитывающая любые закономерности развития явлений, имеет вид:
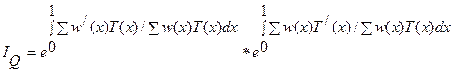, (7.4)
или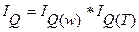 
, (7.5)
где первый сомножитель правой части соотношений (7.4) и (7.5) характеризует степень влияния фактора w на динамику результативного показателя ∑Q, а второй – степень влияния фактора Т.
В случае последовательного изменения факторов темпы роста результативного показателя по факторам в равенстве (7.5) эквивалентны темпам роста, вычисляемым индексным методом.
При одновременном изменении факторов темпы роста по факторам выражаются
а) в предположении линейных тенденций развития аддитивных факторов Q формулами
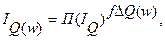и 
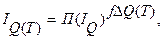если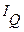 
≠ 1, (7.6)
где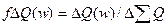 
, 
.
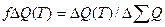или
, 
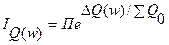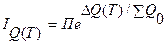, если 
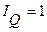, (7.7)
где П – знак произведения по тем же объектам, по которым производится повторное суммирование в исходной модели;
б) в предположении экспоненциального изменения факторов (w, T) формулами
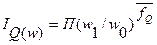, (7.8)
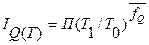, (7.9)
где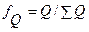 
, 
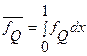- средняя величина удельного веса аддитивного фактора Q за отчетный период.
На практике величина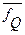 
рассчитывается по приближенным формулам средней хронологической для моментных рядов динамики, например,
.
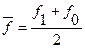В случае применения формул (7.6) – (7.9) для расчета факторных оценок по частям периода [0,1] итоговые факторные оценки за весь период в целом будут равны произведению соответствующих частных факторных оценок.
Приведем пример факторного анализа модели, характеризующей зависимость уровня рентабельности производственных фондов (Рф), исчисляемого как отношение прибыли от реализации товарной продукции к среднегодовой стоимости основных производственных фондов и нормируемых оборотных средств, от рентабельности реализованной продукции (Рп), выраженной долей прибыли в 1 руб. стоимости продукции, фондоотдачи основных производственных фондов по реализованной продукции (Ф) и от коэффициента оборачиваемости оборотных средств (Коб):
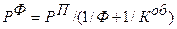
или в развернутом виде -
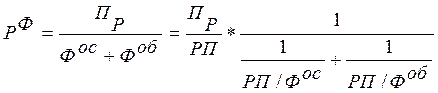, (7.10)
где Пр - прибыль от реализации товарной продукции; Фос – средняя годовая стоимость основных производственных фондов; Фоб – средняя годовая стоимость нормируемых оборотных средств; РП - реализованная товарная продукция.
Поскольку все факторы Рп, Ф, Коб – качественные, мультипликативной цепочки не образуют, то при отсутствии данных о закономерностях их развития вряд ли возможно привести неоспоримые доводы в пользу той или иной последовательности изменения факторов.
Признание же одновременности их развития, что обычно имеет место в действительности, позволяет установить единообразный подход к изучению влияния факторов на динамику результативного показателя на основе интегрального метода. Рассмотрим методику его применения для исследования модели (7.10) на следующем примере.
Исходные данные по заводу технического стекла
(в сопоставимых ценах) для анализа динамики его рентабельности
 № п/п
| Показатели | Периоды | ||
| базисный | отчетный | |||
| Стоимость реализованной товарной продукции в оптовых ценах предприятия, тыс.руб. (РП) | ||||
| Прибыль от реализации продукции, тыс.руб. (Пр) | ||||
| Среднегодовая стоимость основных производственных фондов, тыс.руб. (Фос) | ||||
| Среднегодовая стоимость нормируемых оборотных средств, тыс.руб. (Фоб) | ||||
| Рентабельность производственных фондов, руб. [2:(3+4)] (Рф) | 0,22344 | 0,23551 | ||
| Рентабельность реализованной продукции, руб. (2:1) (Рп) | 0,28166 | 0,21734 | ||
| Фондоотдача основных производственных фондов по реализованной продукции, руб. (1:3) (Ф) | 0,96270 | 1,30660 | ||
| Коэффициент оборачиваемости оборотных средств (1:4) (Коб) | 4,51015 | 6,34972 | ||
| Доля основных производственных фондов в общей величине фондов [3: (3+4)] (fос) | 0,82411 | 0,82934 | ||
| Доля оборотных средств в общей величине фондов [4: (3+4)] (fоб) | 0,17589 | 0,17066 | ||
Для разложения индекса рентабельности производственных фондов интегральным методом используем формулу (7.8):
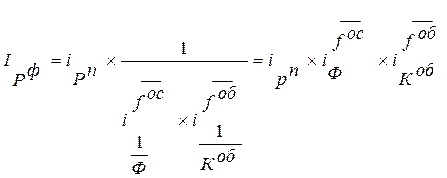, (7.11)
где fос = (I/ф)/(I/ф+I/Коб) = (Фос/РП)/(Фос/РП+Фоб/РП) = Фос/(Фос+Фоб),
,
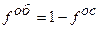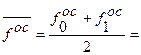(0,82411 + 0,82934)/2 = 0,82672 (см. строку 9 в таблице)
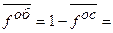0,17328.
Каждый из сомножителей правой части формулы (7.11) характеризует степень влияния соответствующего фактора на динамику рентабельности производственных фондов. Рассчитаем их по данным таблицы, расположенным в строках 6-8:
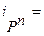0,21734/0,28166 = 0,772;
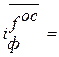(1,30660/0,96270)0,82672 = 1,287,
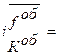(6,34972/4,51015)0,17328 =1,061.
Для проверки правильности полученных результатов вычислим левую и правую части формулы (7.11):
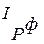= 0,23551/0,22344 = 1,054,
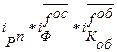= 0,772 1*1,287*1,061 = 1,054.
Их равенство означает, что расчеты произведены верно. Исходя из величины факторных оценок, можно заключить, что рентабельность производственных фондов за отчетный период изменилась за счет факторов следующим образом: в результате снижения рентабельности реализованной продукции она уменьшилась на 22,8%; за счет увеличения фондоотдачи возросла на 28,7%; в результате увеличения коэффициента оборачиваемости оборотных фондов увеличилась на 6,1%. В целом за счет действия всех факторов результативный показатель увеличился на 5,4%.
ЗАДАЧА 190
Приведены данные, характеризующие выпуск продукции и стоимость основных производственных фондов промышленного предприятия за первый квартал предшествующего и отчетного годов (тыс. руб.):
| Показатели | 1 квартал 1999 г. | План на 1 квартал 2000 г. | Отчет за 1 квартал 2000 г. |
| Чистая продукция Стоимость основных производственных фондов на: 1 января 1 февраля 1 марта 1 апреля | 5 350 5 740 5 760 5 775 5 790 | 5 480 5 825 5 840 5 865 5 880 | 5 870 5 680 5 695 5 720 5 745 |
На основании приведенных данных требуется:
1. Определить среднюю стоимость основных производственных фондов.
2. ОПРЕДЕЛИТЬ фондоемкость (в коп.).
3. Интегральным методом измерить влияние на изменение выпуска чистой продукции в отчетном периоде в сравнении с планом и предшествующим периодом следующих факторов: а) изменения средней стоимости основных производственных фондов; б) изменения фондоемкости.
4. Составить обобщающую таблицу и проанализировать исчисленные показатели.
ЗАДАЧА 191
Приведены данные по промышленному предприятию (тыс. руб.):
| Показатели | Предшествующий период (1999 г.) | План на 2000 г. | Отчет за 2000 г. |
| Товарная продукция Затраты предметов труда на производство продукции | 103 520 48 100 | 107 280 49 100 | 110 340 50 980 |
На основании приведенных данных требуется:
1. Исчислить материалоемкость (затраты предметов труда на 1 руб. товар
ной продукции, коп.).
2. Интегральным методом измерить влияние на изменение выпуска товарной продукции в отчетном периоде в сравнении с планом и предшествующим периодом следующих факторов: а) изменения количества предметов труда, потребленных в производстве; б) изменения материалоемкости.
3. Определить относительную экономию (перерасход) материальных затрат
отчетного периода в сравнении с планом и предшествующим периодом.
4. Составить обобщающую таблицу и проанализировать исчисленные показатели.
ЗАДАЧА 192
Приведены данные по промышленному предприятию:
| Показатели | Предшествующий период (1999 г.) | План на 2000 г. | Отчет за 2000 г. |
| Среднеквартальная численность промышленно-производственного персонала, чел. Стоимость основных производственных фондов (тыс. руб.) на: 1 января 1 февраля 1 марта 1 апреля | 14 620 68 300 69 000 69 100 69 230 | 14 750 69 570 70 010 70 120 70 170 | 14 680 69 300 69 670 70 050 70 140 |
На основании приведенных данных требуется:
1. Определить среднюю квартальную стоимость основных производственных фондов.
2. Исчислить фондовооруженность труда (среднеквартальную стоимость основных производственных фондов на одного работающего).
3. Интегральным методом измерить влияние на изменение фондовооруженности в отчетном периоде в сравнении с планом и предшествующим периодом следующих факторов: а) изменения среднеквартальной численности промышленно-производственного персонала; б) изменения средней стоимости основных производственных фондов.
4. Составить обобщающую таблицу и проанализировать исчисленные показатели.
ЗАДАЧА 193
Приведены данные, характеризующие выпуск продукции и среднегодовую численность рабочих промышленного предприятия:
| Показатели | Предшествующий период (1999 г.) | План на 2000 г. | Отчет за 2000 г. |
| Чистая продукция, тыс. руб. Среднегодовая численность рабочих, чел. | 58 600 7 935 | 59 000 7 960 | 59 730 7 981 |
На основании приведенных данных требуется:
1. Определить среднегодовую выработку чистой продукции на одного рабочего (в руб.).
2. Интегральным методом измерить влияние на изменение выпуска чистой продукции в отчетном периоде в сравнении с планом и с предшествующим периодом следующих факторов: а) изменения среднегодовой численности рабочих; б) изменения среднегодовой выработки чистой продукции на одного рабочего.
