| х | |||
| f(x) |

Поиск: Рекомендуем:  Почему я выбрал профессую экономиста
Почему я выбрал профессую экономиста
 Почему одни успешнее, чем другие
Почему одни успешнее, чем другие
 Периферийные устройства ЭВМ Периферийные устройства ЭВМ
 Нейроглия (или проще глия, глиальные клетки) Нейроглия (или проще глия, глиальные клетки)
Категории:
|
Какой многочлен является интерполирующим для данной функции?
| 1) P2(x)= 2 х + 2 х2 2) P2(x)= - 2 х - 2 х2 3) P2(x)= - 2 х + 2 х2 | |||||||||||||||
|
Какой многочлен является интерполирующим для данной функции?
| 1) P2(x)= х + 3 х2 2) P2(x)= 5х - 3 х2 3) P2(x)= - х + 3 х2 | ||||||||||||||||
|
Какой многочлен является интерполирующим для данной функции?
| 1) P2(x)= -1 - 2 х + 3 х2 2) P2(x)= 1 - 2 х - 3 х2 3) P2(x)= 1 - 2 х + 3 х2 | ||||||||||||||||
| 33. При разложении нечетной функции в ряд Фурье | 1) Все an = 0 2) Нечетные коэффициенты a2n-1 = b2n-1 = 0, остальные отличны от нуля 3) Четные коэффициенты a2n = b2n = 0,остальные отличны от нуля 4) Все bn = 0 | ||||||||||||||||
| 34.Ряд Фурье функции f(x) = x при -1< x < 1 и периодически продолженной влево и вправо равен: | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||||||||
В разложении периодической с периодом T функции f(x) в ряд Фурье  коэффициенты an равны: коэффициенты an равны:
| 1)  2)
2) 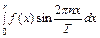 3)
3)  4)
4)  5)
5) 
| ||||||||||||||||
| Следующие функции являются периодическими: | ¨ cos 1,5x ¨ sin x ¨ tg x ¨ x2 ¨ ln x ¨ ex | ||||||||||||||||
Тригонометрический ряд Фурье  , с коэффициентами , с коэффициентами  сходится равномерно к периодической с периодом T функции f(x), если: сходится равномерно к периодической с периодом T функции f(x), если:
| 1) функция f(x) интегрируема 2) функция f(x) непрерывна во всех точках x 3) функция f(x) непрерывна вместе со своей производной во всех точках x 4) функция f(x) дифференцируема во всех точках x | ||||||||||||||||
| Ряд Фурье функции f(x) = sin2x равен: | 1)  2)
2)  3)
3)  4)
4) 
| ||||||||||||||||
| При разложении четной функции в ряд Фурье: | 1) четные коэффициенты a2n = b2n = 0, остальные отличны от нуля 2) все bn = 0 3) все an = 0 4) нечетные коэффициенты a2n-1 = b2n-1 = 0, остальные отличны от нуля | ||||||||||||||||
| Ряд Фурье функции f(x) = |x| при -1<x<1 и периодически продолженной влево и вправо равен: | 1)  2)
2)  3)
3)  4)
4) 
|
ГЛОССАРИЙ
Тригонометрическим рядом называется функциональный ряд вида:

где действительные числа  называются коэффициентами ряда.
называются коэффициентами ряда.
Числа аn, bn – называются коэффициентами Фурье, а тригонометрический ряд  - рядом Фурье функции f(x).
- рядом Фурье функции f(x).
Модуль разности между точным значением х и его приближенным значением а называется абсолютной погрешностью приближенного значения х и обозначается  :
:
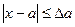 ,
,  .
.
Цифра m приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра m.
Цифра m приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра m.
Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными.
Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой.
Относительной погрешностью  приближеного значения а числа х называется отношение абсолютной погрешности
приближеного значения а числа х называется отношение абсолютной погрешности 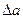 этого приближения к числу а, т.е.
этого приближения к числу а, т.е.  .
.
Апроксимация – это замена некоторой функции, заданной аналитически или таблично, другой функцией, близкой к исходной, но более простой и удобной для вычислений.
Экстраполяция приближённое определение значений функции f (x) в точках x, лежащих вне отрезка[ x 0; x n], по её значениям в точках x 0< x 1<…< x n-1< x n.
Интерполяция — это способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.
|
|
|
|
|
|
Дата добавления: 2017-03-12; Мы поможем в написании ваших работ!; просмотров: 798 | Нарушение авторских прав
Лучшие изречения: