Основные вопросы: Понятие кусочно-непрерывного интерполяционного многочлена, сплайна. Степень, дефект сплайна. Сплайн-функция. Определение. Свойства. Построение интерполяционного сплайна третьего порядка.
Краткие теоретические сведения: При большом количестве узлов интерполяции сильно возрастает степень интерполируемых многочленов, что делает их не удобными для вычислений. Высокой степени многочлена можно избежать разбив отрезок интерполяции на несколько частей с последующим построением не каждой части самостоятельного интерполяционного многочлена, однако такое интерполирование имеет недостаток: в точках стыка разных интерполяционных многочленов будет разрывной их первая производная. В этом случае удобно использовать особый вид кусочно-полиномиальной интерполяции – интерполяция сплайнами.
Сплайн – это функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом.
Пусть  – интерполируемый сплайн порядка m для функции
– интерполируемый сплайн порядка m для функции 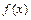 заданной таблично
заданной таблично

| 
| 
| … | 
|

| 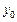
| 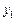
| … | 
|
Если выполняются условия:
1. На каждом из отрезков 

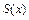 – многочлен порядка m.
– многочлен порядка m.
2. 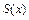 и ее производные до
и ее производные до  порядков включительно непрерывны на отрезке
порядков включительно непрерывны на отрезке 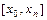
3.  ,
,  – непосредственное условие интерполирования
– непосредственное условие интерполирования
Общий вид сплайнов для функции 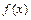 :
:
 , где
, где  – многочлен 3-ей степени
– многочлен 3-ей степени

Для построения кубического сплайна необходимо построить n многочленов третьей степени, т.е. определить 4n неизвестных ai, bi, ci, di. Эти коэффициенты ищутся из условий в узлах сетки:

В данной системе предполагается, что сплайны имеют нулевую кривизну на концах отрезка. В общем случае могут быть использованы и другие условия.
Если ввести обозначение hi = xi – xi-1 и исключить из системы неизвестные ai, bi, di, то можно получить системы из (n – 1) линейных алгебраических уравнений относительно ci, i = 2,…, n, с трехдиагональной матрицей:
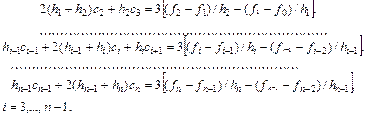
Остальные коэффициенты сплайнов могут быть восстановлены по формулам
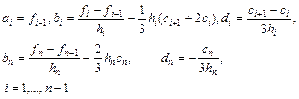
Примеры решения задач:
1. Построить кубический сплайн для функции, заданной в узлах интерполяции, предполагая, что сплайн имеет нулевую кривизну при x=x0 и x=x4; вычислить значение функции f(1.5).
| i | |||||
| xi fi | 0,0 0,0 | 1,0 1,8415 | 2,0 2,9093 | 3,0 3,1411 | 4,0 3,2432 |
Решение. Запишем систему уравнений:
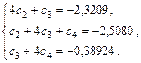
Решив данную систему, найдем c2, c3, c4 и, воспользовавшись формулами, заполним таблицу.
| i | [ xi-1, xi ] | ai | bi | ci | di |
| [0, 1] [1, 2] [2, 3] [3, 4] | 0,0 1,8415 2,9093 3,1411 | 1,9913 1,5418 0,56934 0,07978 | 0,0 – 0,44949 – 0,52299 0,03344 | – 0,14983 – 0,02450 0,18548 – 0,01115 |
Имеем 
Вычислим значение функции f (1,5). Точка x = 1,5 принадлежит отрезку [1, 2], на этом отрезке таблично заданная функция представляется кубическим сплайном:
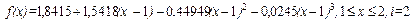 Получаем f (1,5)=2,4969.
Получаем f (1,5)=2,4969.
Порядок выполнения работы
1. Построить кубический сплайн для функции, заданной в узлах интерполяции, предполагая, что сплайн имеет нулевую кривизну при
х = х0 и х = х4. Вычислить значение функции в точке х = Х *.
| Х *=1,5 | х | 1,0 | 1,0 | 2,0 | 3,0 | 4,0 |
| у | 0,0 | 0,5 | 0,86603 | 1,0 | 0,86603 | |
| Х *=1,5 | х | 0,0 | 1,0 | 2,0 | 3,0 | 4,0 |
| у | 1,0 | 0,86603 | 0,5 | 0,0 | -0,5 | |
| 3 Х *=1,5 | х | 0,0 | 0,9 | 1,8 | 2,7 | 3,6 |
| у | 0,0 | 0,36892 | 0,85408 | 0,7856 | 6,3138 | |
| Х *=1,5 | х | 0,0 | 0,9 | 1,8 | 2,7 | 3,6 |
| у | 0,0 | 0,72235 | 1,5609 | 2,8459 | 7,7275 | |
| 5 Х *=1,5 | х | 0,0 | 1,0 | 2,0 | 3,0 | 4,0 |
| у | 1,0 | 1,5403 | 1,5839 | 2,01 | 3,3464 | |
| 6 Х *=0,8 | х | 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
| у | -2,2026 | -0,19315 | 0,79464 | 1,5624 | 2,2306 | |
| 7 Х *=1,5 | х | 0,0 | 1,0 | 2,0 | 3,0 | 5,0 |
| у | 0,0 | 0,2618 | 0,9069 | 1,5708 | 1,3090 | |
| 8 Х *=0,8 | х | 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
| у | 10,1 | 2,5 | 2,0111 | 2,0692 | 2,2882 | |
| 9 Х *=0,8 | х | 0,1 | 0,5 | 0,9 | 1,3 | 1,7 |
| у | 10,0 | 2,0 | 1,1111 | 0,76923 | 0,58824 | |
| х | 0,0 | 1,7 | 3,4 | 5,1 | 6,8 | |
| у | 0,0 | 3,0038 | 5,3439 | 7,3583 | 9,4077 |
Контрольные вопросы
1. Как ставится задача построения интерполяционного сплайнатретьего порядка?
2. Как определяется степень сплайна?
3. Как обосновывается существование и единственность многочлена наилучшего приближения?
4. Как определить параметры интерполяционного сплайнатретьего порядка?
Практическое занятие № 14
Тема: «Линейное интерполирование»
Основные вопровы: Табличная функция. Задача интерполирования табличной функции. Теорема о единственности задачи полиноминального интерполирования. Конечные разности таблиц. Формула линейного интерполирования и способы оценки ее погрешности. Обратное линейное интерполирование.
Краткие теоретические сведения: Пусть имеется таблица значений функции f с постоянным шагом h > 0 и требуется по табличным данным найти f (х) при х, не совпадающем с табличным аргументами. Для этого обозначим через х 0, х1,(х 0<х1) два соседних табличных аргумента, между которыми находится х, через у0, у1 – соответствующие табличные значения, и из первой интерполяционной формулы Ньютона при n =1 получим

Это и есть формула линейного интерполирования.
Пусть вторая производная функции f непрерывна на  . Тогда абсолютные погрешности приближений
. Тогда абсолютные погрешности приближений  к значениям f (х) можно находить с помощью оценочной функции V1:
к значениям f (х) можно находить с помощью оценочной функции V1:
 или
или  , где
, где  и
и  .
.
В случае линейной интерполяции удобно пользоваться общей оценкой погрешностей для всех  . Учитывая, что
. Учитывая, что  при
при  , а также равенство
, а также равенство
 , для абсолютной погрешности функции
, для абсолютной погрешности функции 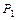 на
на  получим формулу
получим формулу
 .
.
Следовательно,
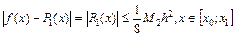 .
.
При оценке погрешностей линейной интерполяции можно избавиться от вычисления  и поиска числа М 2. Для этого установим связь между
и поиска числа М 2. Для этого установим связь между  и конечной разностью второго порядка. Учитывая, что производная
и конечной разностью второго порядка. Учитывая, что производная  непрерывная, то по теореме Лагранжа имеем
непрерывная, то по теореме Лагранжа имеем
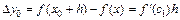 , где
, где  . Далее с помощью этой теоремы найдем выражение для второй разности через
. Далее с помощью этой теоремы найдем выражение для второй разности через 
 ,
,
где число  .
.
В силу непрерывности  на
на  при малом шаге h с большей степенью точности можно считать, что
при малом шаге h с большей степенью точности можно считать, что  для всех
для всех  . Отсюда вытекает, что
. Отсюда вытекает, что
 или
или  ,
,
а также  . Полученные соотношения позволяют применять достаточно хорошую приближенную оценку:
. Полученные соотношения позволяют применять достаточно хорошую приближенную оценку:
 .
.
Данная оценка позволяет вывести правило определения верных цифр непосредственно по таблице конечных разностей. Пусть к – номер разряда десятичной записи числа  . Если разряд в целой части числа, то к>0, если в дробной, то к< 0. Цифра в к -м разряде верная, если
. Если разряд в целой части числа, то к>0, если в дробной, то к< 0. Цифра в к -м разряде верная, если  .Это условие можно считать выполненным, как только окажется
.Это условие можно считать выполненным, как только окажется  . Отсюда следует правило.
. Отсюда следует правило.
Правило. Если на каком-либо участке таблицы модули конечных разностей второго порядка имеют в к -м разряде не более четырех единиц, то у приближенных значений функции f, найденных с помощью линейного интерполирования для х из этого участка, цифры к -го разряда будут верными.
На практике часто приходится решать задачу: дано какое-то значение у функции f, не равное табличным значениям уi, и необходимо найти соответствующий аргумент х. То есть нужно вычислить значение обратной по отношению к у = f (х) функции, обозначим ее  .
.
Формула обратного линейного интерполирования

Для вычисления с ее помощью при заданном у выбираются два соседних табличных значения функции f, между которыми находится у, и предыдущее значение принимается за у0, а последующее – за у1.
Остаточный член формулы выглядит следующим образом:
 ,
,
где  , у находится между у0 и у1.
, у находится между у0 и у1.
Общая оценка погрешности формулы для всех у, находящихся между у0 и у1, обеспечивается неравенством

Примеры решения задач
1. Вычислить значение  с помощью линейной интерполяции.
с помощью линейной интерполяции.
Решение. Возьмем х 0=1,1, х 1=1,2. Тогда у 0=0,891, у 1=0,9333,  . Шаг таблицы h =0,1. Для определения точности воспользуемся всеми тремя полученными оценками. Цифры табличных значений функции будем считать верными.
. Шаг таблицы h =0,1. Для определения точности воспользуемся всеми тремя полученными оценками. Цифры табличных значений функции будем считать верными.
Таблица 1
| х | 
| 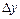
| 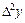
|
| 1,0 | 0,841 | 0,050 | -0,008 |
| 1,1 | 0,891 | 0,042 | -0,011 |
| 1,2 | 0,933 | 0,031 | |
| 1,3 | 0,964 |
Поскольку 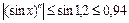 для всех
для всех  , берем М 2=0,94.
, берем М 2=0,94.
 .
.
Так как  , следовательно
, следовательно
 .
.
При х =1,11 будет t =0,1, поэтому  .
.
Найдем искомые приближения:
 .
.
Без учета вычислительных погрешностей числа а имеет верные цифры 8, 9 и 5.
Порядок выполнения работы
1. Найдите приближения  и
и 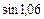 линейным интерполированием и исследуйте погрешность.
линейным интерполированием и исследуйте погрешность.
2. По таблице 1 обратным линейным интерполированием найдите  и определите верные значащие цифры полученного приближенного значения.
и определите верные значащие цифры полученного приближенного значения.
Контрольные вопросы
1. Формулы линейного программирования и способы оценки ее погрешности.
2. Сформулирцйте правило пределения верных значащих цифр с помощью таблицы конечных разностей при линейном интерполировании.
3. Как вычисляются значения обратной для f функции  для аргументов по формуле обратного линейного интерполирования.
для аргументов по формуле обратного линейного интерполирования.
Практическое занятие № 15
Тема: «Задача приближенного вычисления определенных интегралов»
Основные вопросы: Постановка задач численного интегрирования. Формула прямоугольников, вывод формулы. Вывод квадратурной формулы трапеций. Квадратурная формула Симпсона. Оценка погрешности.
Краткие теоретические сведения:Пусть задана функция f (x) в виде таблицы
| x | x0 | x1 | ……. | xn |
| f(x) | y0 | y1 | ……. | yn |
Найти интеграл от этой функции, т.е.
 ,
,  ,
, 
Эту задачу будем решать методом численного интегрирования путём замены под интегральный функции её интерполяционным многочленом, и найдём приближённое значение этого интеграла.
Используем интерполяционный многочлен степени n=1.
Вывод квадратурной формулы трапеции для линейной функции:
| x0 | x1 |
| y0 | y1 |
постоянный шаг 
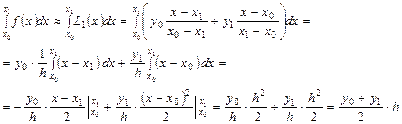
 - квадратурная формула трапеции
- квадратурная формула трапеции
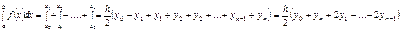
 – общая квадратурная формула трапеции
– общая квадратурная формула трапеции
Оценка погрешности
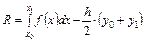 , n=2 и
, n=2 и 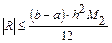
Квадратурная формула Симпсона (или парабола)

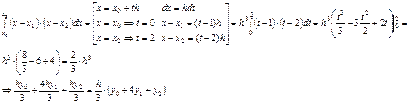
 – квадратурная формула Симпсона (параболы)
– квадратурная формула Симпсона (параболы)
Выведем общую формулу Симпсона
 , n -чётное
, n -чётное

 – Общая квадратурная формула Симпсона
– Общая квадратурная формула Симпсона
Оценка погрешности
 , где
, где 
Примеры решения задач
1. Вычислить интеграл от функции  на отрезке
на отрезке  по формулам трапеций и Симпсона при делении отрезка на 6 равных частей. Оценить погрешность методом интегрирования.
по формулам трапеций и Симпсона при делении отрезка на 6 равных частей. Оценить погрешность методом интегрирования.
Решение: Найдем по формуле  ,
, 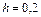 и составим таблицу значений функции
и составим таблицу значений функции 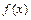 в точках
в точках  , т. е.
, т. е. 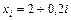
| x | 2,2 | 2,4 | 2,6 | 2,8 | 3,0 | 3,2 | |
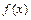
| 3,22732 | 3,16704 | 3,11726 | 3,07625 | 3,04272 | 3,01568 | 2,99429 |
Общая формула трапеций принимает вид:

Проведем вычисления:

Т.к. число 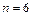 четное, то можно применить метод Симпсона
четное, то можно применить метод Симпсона

Проведем вычисления

Ответ: 3,70595; 3,70516
Порядок выполнения работы
1. Вычислить интеграл  , приняв шаг интегрирования
, приняв шаг интегрирования  , с помощью:
, с помощью:
1) формул прямоугольника;
2) формулы трапеций;
3) формулы Симпсона;
4) сравнить полученные результаты с точным решением (найти его самостоятельно), определить абсолютную и относительную погрешности каждого метода.
Контрольные вопросы
1. Формулы прямоугольников, погрешность формул прямоугольников.
2. Формула трапеций, погрешность метода трапеций.
3. Формула Симпсона, погрешность метода Симпсона.
Практическое занятие № 16.
Тема: «Численное дифференцирование»
Основные вопровы: Постановка задачи численного дифференцирования. Формулы численного дифференцирования на основе интерполяционного многочлена Ньютона. Безразностные формулы численного дифференцирования для равноотстоящих узлов. Применение ряда Тейлора для численного дифференцирования.
Краткие теоретические сведения: Пусть задана таблица значений функций с равноотстоящими узлами и шагом h:
| x | x0 | x1 | … | xn |
| f(x) | y0 | y1 | … | yn |
где xi=x0+ih, i=1,2,…,n. Для нахождения значения производной функции в промежуточной точке, расположенной ближе к началу таблицы, функцию f(x) заменяют приближенно первым интерполяционным многочленом Ньютона:
 где
где 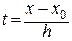 (заметим, что в качестве x0 выбирается ближайший к точке x слева узел интерполяции). Продифференцировав приближенное равенство по переменной t, получим приближенную формулу для вычисления производной таблично заданной функции в промежуточной точке:
(заметим, что в качестве x0 выбирается ближайший к точке x слева узел интерполяции). Продифференцировав приближенное равенство по переменной t, получим приближенную формулу для вычисления производной таблично заданной функции в промежуточной точке:
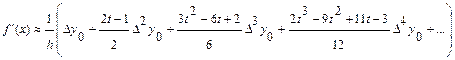 Для вычисления производной в точке, расположенной ближе к концу таблицы, следует использовать второй интерполяционный многочлен Ньютона. Применяя тот же прием, получим:
Для вычисления производной в точке, расположенной ближе к концу таблицы, следует использовать второй интерполяционный многочлен Ньютона. Применяя тот же прием, получим:
 Примеры решения задач
Примеры решения задач
Вычислить значение производной в точке x=0,12 функции, заданной таблично, используя интерполяционные формулы Ньютона. Найти значение производной функции в точке x из её аналитического выражения и вычислить абсолютную погрешность.
Решение:
| x | 0,05 | 0,15 | 0,25 | 0,35 | 0,45 | 0,55 | 0,65 |

| 0,9968 | 0,9888 | 0,9689 | 0,9394 | 0,9004 | 0,8525 | 0,7961 |
Составим таблицу конечных результатов
| i | 
| 
|

|

|

|

|
| 0,05 | 0,9988 | -0,01 | -0,0099 | 0,0003 | -0,0002 | |
| 0,15 | 0,9888 | -0,0199 | -0,0096 | 0,0001 | 0,0005 | |
| 0,25 | 0,9689 | -0,0295 | -0,0095 | 0,0006 | -0,0002 | |
| 0,35 | 0,9394 | -0,039 | -0,0089 | 0,0004 | ||
| 0,45 | 0,9004 | -0,0479 | -0,0085 | |||
| 0,55 | 0,8525 | -0,0564 | ||||
| 0,65 | 0,7961 |






