Предисловие
Данные методические рекомендации предназначены для подготовки магистров по направлению 110800 Агроинженерия.
В современной науке и технике математические методы исследования и проектирования играют все большую роль. Общий курс математики является фундаментом инженерного образования. Внедрение вычислительной техники существенно расширяет возможности применения математики при решении конкретных задач. Темпы развития науки и техники делают невозможной подготовку специалистов, имеющих готовые рецепты для решения всех задач, с которыми им придется сталкиваться. В соответствии с ФГОС ВПО, область профессиональной деятельности магистров включает в себя эффективное использование и сервисное обслуживание сельскохозяйственной техники, машин и оборудования, средств электрификации и автоматизации технологических процессов при производстве, хранении и переработке продукции растениеводства и животноводства; разработку технических средств для технологической модернизации сельскохозяйственного производства.
Поэтому математическое образование инженера должно быть широким, общим, то есть мало специализированным, достаточно фундаментальным, иметь четко выраженнуюприкладную направленность, быть в известной мере индивидуализированным.
Фундаментальность математической подготовки включает в себя достаточную общность математических понятий и конструкций, обеспечивающую широкий спектр их применимости, разумную точность формулировок математических свойств изучаемыхобъектов, логическую строгость изложения математики, опирающуюся на адекватный современный математический язык.
Предметом изучения прикладной математики являются количественные отношения и пространственные формы действительного мира. Главная особенность ее, как указывалось выше, состоит в том, что она является важнейшей составляющей фундаментальной подготовки инженера. При этом математика является не только мощным средством решения прикладных задач и универсальным языком науки, но также и элементом общей культуры.
К каждому практическому занятию приведены основные теоретические сведения, решение типовых примеров и задач, задачи для самостоятельного решения с ответами. По каждому разделу предусмотрены зачетные работы в форме контрольной работы.
Практические занятия
Практическое занятие № 1
Тема: Понятие ряда Фурье. Сходимость ряда Фурье.
Основные вопросы: Периодические функции. Периодические процессы. Постановка задачи и определение ряда Фурье. Коэффициенты Фурье. Разложение в ряд Фурье 2π-периодических функций. Теорема Дирихле.
Краткие теоретические сведения: При изучении разнообразных периодических процессов, т. е. процессов, которые через определенный промежуток времени повторяются, целесообразнее разлагать периодические функции, описывающие эти процессы, не в степенной ряд, а в так называемый тригонометрический ряд.
Определение 1: Тригонометрическим рядом называется функциональный ряд вида:
 (1)
(1)
где действительные числа  называются коэффициентами ряда.
называются коэффициентами ряда.
В отличии от степенного ряда в тригонометрическом ряде вместо простейших функций 1, х, х2,…, хn,… взяты тригонометрические функции
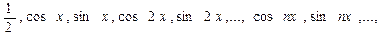 (2)
(2)
которые тоже хорошо изучены.
Система функций (2) называется основной тригонометрической системой. Любая частичная сумма ряда (1) 2π – периодична. Отсюда следует, что если ряд (1) сходится на отрезке [-π; π], то он сходится на всей числовой прямой и его сумма, будучи пределом последовательности частичных сумм, является периодической функцией с периодом Т =2π. По этой причине тригонометрические ряды особенно удобны при изучении периодически функций, описывающих различные периодические процессы. Например процессы колебательных и вращательных движений различных деталей машин и приборов, периодическое движение небесных тел и элементарных частиц, акустические и электромагнитные колебания и др.
Функция (2) обладает еще свойством ортогональности на отрезке [-π; π]:
 Далее:
Далее:
 , при k ≠ n.
, при k ≠ n.
Если k=n, то
 Аналогично находим
Аналогично находим

Наконец 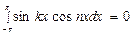
Так как
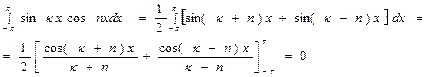
при k≠n.
Если k=n, то  .
.
Для тригонометрического ряда, как и для степенного ряда, можно установить условия разложения функций.
Теорема 1. Пусть 2π периодическая функция f(x) интегрируема на отрезке [-π; π]. Тогда, если на отрезке [-π; π] функция f(x) раскладывается в тригонометрический ряд
 , (3)
, (3)
который можно интегрировать почленно, то это разложение единственно, а его коэффициенты находятся по формулам:
 ,
, 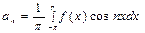 ,
,  . (4)
. (4)
Определение 2. Пусть f(x) – 2π-периодическая функция, интегрируемая на отрезке [-π; π]. Тогда числа аn, bn – называются коэффициентами Фурье, а тригонометрический ряд  - рядом Фурье функции f(x).
- рядом Фурье функции f(x).
Установим, при каких условиях ряд Фурье функции f(x) сходится к этой функции.
Теорема 2. Пусть 2π-периодическая функция f(x) и ее производная  - непрерывные функции на отрезке [-π; π] или же имеют на нем конечное число точек разрыва первого рода. Тогда ряд Фурье функции f(x) сходится на всей числовой прямой, причем его сумма S(x) = f(x), если х – точка непрерывности функции f(x). Если х0 – точка разрыва f(x), то
- непрерывные функции на отрезке [-π; π] или же имеют на нем конечное число точек разрыва первого рода. Тогда ряд Фурье функции f(x) сходится на всей числовой прямой, причем его сумма S(x) = f(x), если х – точка непрерывности функции f(x). Если х0 – точка разрыва f(x), то
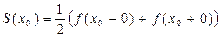 ,
,
где
 .
.
Примеры решения задач
Пример1. Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f (х), заданную на отрезке [-π; π].
 .
.
Решение: Данная функция удовлетворяет условиям теоремы 2 и, следовательно, может быть разложена в ряд Фурье. Найдем коэффициенты Фурье.
По формулам (4) находим
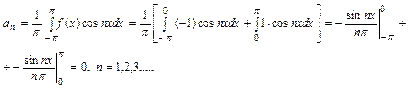

 .
.
Разложение для данной функции будет

Это равенство справедливо во всех точках, кроме точек разрыва  . В точках
. В точках  сумма ряда равна
сумма ряда равна  .•
.•
Если функция f(x) 2π-периодичная, то при вычислении ее коэффициентов Фурье интегрирование можно выполнять по любому отрезку длиной 2π, например, на промежутке [0; 2π].
Пример 2. Разложить в ряд Фурье функцию  с периодом Т = 2π на промежутке [0; 2π].
с периодом Т = 2π на промежутке [0; 2π].
Решение: график функции изображен на рисунке
| |||
| Рисунок 1 |
Эта функция на отрезке  задается формулами:
задается формулами:  ,
,  и
и  ,
,  . В то же время на
. В то же время на  гораздо проще она задается одной формулой
гораздо проще она задается одной формулой  . Поэтому, интегрируя по отрезку
. Поэтому, интегрируя по отрезку  , получаем:
, получаем:
 .
. 
 Следовательно,
Следовательно, 
Этот ряд дает задает функцию во всех точках, кроме точек разрыва  .
.
В этих точках сумма ряда равна:

Порядок выполнения работы
1. Разложить в ряд Фурье функцию:  ,
,
и построить график суммы ряда Фурье.
2. Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f (х), заданную на отрезке [-π; π]
 .
.
3. Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f (х) = 2 х +3, заданную на отрезке [-π; π]
4. Разложить в ряд Фурье периодическую (с периодом Т = 2π) функцию f (х), заданную на отрезке [-π; π]
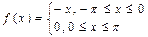 .
.
Ответы: 1)  .
.
2)  . 3)
. 3)  .
.
4) 
Контрольные вопросы
- Сформулируйте определение тригонометрического ряда, тригонометрического ряда Фурье.
- Сформулируйте теоремы о сходимости в точке ряда Фурье кусочнонепрерывной, непрерывной функций.
- Опишите идеологию разложения в ряд Фурье непериодических функций.
- Сформулируйте определение интеграла Фурье, признаки сходимости.
- Сформулируйте определение преобразования Фурье.
Практическая работа № 2
Тема: «Ряд Фурье для четных и нечетных функций»
Основные вопросы: Понятие неполных тригонометрических рядов. Коэффициенты разложения в ряд Фурье четных и нечетных функций. Разложение функций, заданных на отрезке [ а; а+2π ].
Краткие теоретические сведения: Если f(-x) = f(x), т. е. f(x) – функция четная, то  и
и
 и
и 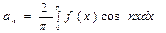 .
.
Если f(-x) = - f(x) т. е. f(x) – функция нечетная, то  и
и
 и
и 
Полученные формулы позволяют упрощать вычисления при нахождении коэффициентов Фурье в тех случаях, когда заданная функция является четной или нечетной.
Примеры решения задач
Пример 1. Разложить в ряд Фурье функцию  .
.
Решение. Рассмотрим 2π-периодическую функцию, которая на [-π; π] задана формулой  . Так как функция f(x) четная, то
. Так как функция f(x) четная, то
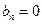 ,
,  ,
,
 , интегрируем дважды по частям, получаем
, интегрируем дважды по частям, получаем

 , n =1, 2, 3,….
, n =1, 2, 3,….
Значит, ряд Фурье данной функции имеет вид

Это равенство справедливо при любом  , так как функция f(x) непрерывна на всей числовой оси. в частности, при
, так как функция f(x) непрерывна на всей числовой оси. в частности, при  имеем
имеем 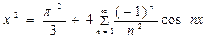
Пример 2. Разложить в ряд Фурье функцию f(x) = х, если 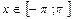 .
.
Решение. График функции с ее периодическим продолжением изображен на рисунке:
 |
|
Рисунок 2
Заданная функция удовлетворяет условиясм Дирихле, поэтому ее можно разложить в ряд Фурье. На промежетке  функция f(x) = х – нечетная, поэтому аn = 0 и разложим функцию по синусам.
функция f(x) = х – нечетная, поэтому аn = 0 и разложим функцию по синусам.

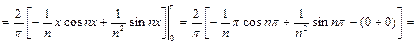
 ,
,
откуда 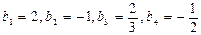 , ….
, ….
получаем, что функцию f(x) = х можно представить в виде
 или
или
 .
.
Это равенство имеет место в точках непрерывности функции f(x), т. е. во всех внутренних точках  . Вне этого промежутка этот ряд изображает периодическое продолжение данной функции.
. Вне этого промежутка этот ряд изображает периодическое продолжение данной функции.
В точках разрыва 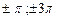 ,… сумма ряда равна среднему арифметическому ее пределов справа и слева в данных точках.
,… сумма ряда равна среднему арифметическому ее пределов справа и слева в данных точках.
В точке 

и в 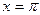
 . Найдем среднее арифметическое этих пределов:
. Найдем среднее арифметическое этих пределов:
 .
.
Во всех точках разрыва получим то же значение, т. е. сумма ряда равна нулю.
Полученное разложение можно записать и в таком виде:

Пример 3. Разложить в ряд Фурье периодическую функцию

Решение. В промежутке 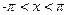 заданная функция – нечетная.
заданная функция – нечетная.
Такую функцию называют ступенчатой. Ее ряд Фурье содержит только синусы.
Найдем коэффициенты bn:
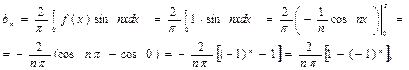
откуда  ….
….
В итоге получаем
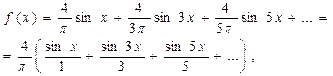
т. е.

В точках разрыва  сумма ряда равна
сумма ряда равна  .
.
Точкой разрыва функциии является точка х=0. Учитывая условия теоремы Дирихле в этой точке сумма ряда равна нулю

Пример 4. разложите в ряд Фурье по косинусам периодическую функцию с периодом  , заданную в промежутке
, заданную в промежутке  слудующим образом:
слудующим образом:
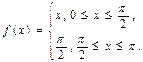
Решение. Функция f(x) задана на промежутке  , но так как ее надо разложить только по косинусам, то в промежутке
, но так как ее надо разложить только по косинусам, то в промежутке  функцию f(x) нужно доплнить ее четным продолжением.
функцию f(x) нужно доплнить ее четным продолжением.
Найдем коэффициенты а0 и аn.
 ,
,
 .
.
Вычислим первый интеграл по частям, предположив, что 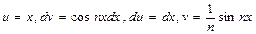 , имеем
, имеем

 .
.
Вычислим второй интеграл:
 .
.
Значит, 
 ,
,
откуда 
Подставив значения  в формулу (1), получим
в формулу (1), получим

Порядок выполнения работы
1. Разложите в ряд Фурье периодическую функцию  при
при  .
.
2. В промежутке  разложите в ряд Фурье по косинусам функции:
разложите в ряд Фурье по косинусам функции:
а)  ; б)
; б)  в)
в) 
г) 
Ответ: 1) 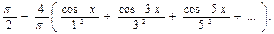
2) а)  .
.
б) 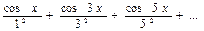 .
.
в) 
г) 
Контрольные вопросы
1. По каким функциям разлагается в ряд Фурье четная (нечетная) функция.
Практическая работа № 3
Тема: «Ряд Фурье с произвольным периодом»
Основные вопросы: Коэффициенты разложения функции с произвольным периодом. Разложение в ряд Фурье функций произвольного периода.
Краткие теоретические сведения: Если функция f (x) в промежутке – l <x< l, где l - произвольное число (l >0), удовлетворяет условиям Дирихле, то ее разложение в ряд Фурье имеет вид
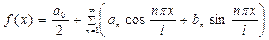 , (5)
, (5)
где
 ,
,  ,
,  .(6)
.(6)
Ряд (6) представляет собой функцию с периодом 2 l, т. е. f (x +2 l)= f (x).
Если f (x) – нечетная функция, то ее ряд Фурье содержит только синусы:
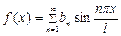 , где
, где  . (7)
. (7)
Если же f (x) – четная функция, то ее ряд Фурье содержит только свободный член и косинусы:
 , где
, где  ,
,  . (8)
. (8)
Примеры решения задач
Пример 1. Разложить в ряд Фурье функцию, заданную в промежутке  уравнением
уравнением  .
.
Решение. Данная функция является четной. Графиком функции служит дуга параболы, заключенная между точками (-1; 1) и (1; 1).
|
Рисунок 3
 ,
, 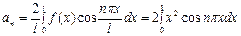 .
.
Интегрируем по частям:  ; тогда
; тогда
 .
.
Снова интегрируем по частям:  , откуда
, откуда

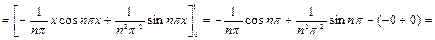
 .
.
Подставив это значение в  в (5),получим
в (5),получим

или  .
.
Пример 2. Разложить в ряд Фурье периодическую (с периодом Т = 2) функцию f (х), заданную на отрезке [-1; 1].

 |
Рисунок 4
Решение. Функция удовлетворяет условиям Дирихле, а поэтому разлагается в ряд Фурье, коэффициенты которого вычислим по известным формулам.
 ,
,
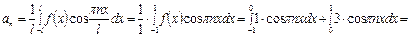
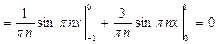 ,
,



Ответ:  .
.
Пример 3. Разложить в ряд Фурье периодическую функцию f (х) =│ x │, на отрезке [-2; 2].

Рисунок 5
Решение. f (х) =│ x │, непрерывная функция, удовлетворяющая условиям теоремы о разложимости, и, следовательно, разлагается в свой ряд Фурье. Она четная, поэтому разлагается в ряд Фурье только по косинусам, т. е. bn = 0.
Находим коэффициенты а 0 и ап искомого ряда
 ,
,
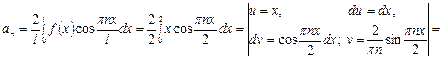


Ответ: искомый ряд Фурье данной функции
 .
.
Пример 4. Пусть требуется разложить в ряд Фурье периодическую функцию f (х) с периодом Т =2, которая на отрезке [-1; 1] задается равенством f (х) =│ x │.
 |
Рисунок 6
Решение. Так как рассматриваемая функция четная l =1, то  ,
, 
 .
.








