Т.к. конечные разности 4-го порядка почти постоянные, то влияние конечных разностей старшего порядка незначительно. Поэтому вычисление производной проведем по формуле:
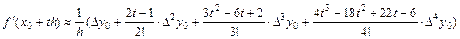
Т.к. ближайший слева от x=0,12 узел 
.
Значение t найдем из равенства 
Аналитическое выражение функции: 
Поэтому точное значение 
Абсолютная погрешность равна
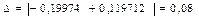
Ответ: 
, 
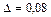
Порядок выполнения работы: Вычислить значение производной в точке x=0,62 функции, заданной таблично, используя интерполяционные формулы Ньютона. Найти значение производной функции в точке x=0,62 из ее аналитического выражения и вычислить абсолютную погрешность.
| x | 0,6 | 0,7 | 0,8 | 0,9 | 1,0 | 1,1 | 1,2 |
| sinx | 0,5646 | 0,6442 | 0,7174 | 0,7833 | 0,8415 | 0,8912 | 0,9320 |
| x | 0,05 | 0,15 | 0,25 | 0,35 | 0,45 | 0,55 | 0,65 |
| cos x | 0,9988 | 0,9888 | 0,9689 | 0,9394 | 0,9004 | 0,8525 | 0,7961 |
Контрольные вопросы
1. В каких случаях прибегают к приближенному дифференцированию?
2. Как по табличным данным можно находить аналитическое выражение производной?
3. Что представляет собой интерполяционная формула Ньютона?
4. Как составляют таблицу конечных разностей для данной функции?
5. В чем заключается неккоректность задачи численного дифференцирования?
6. В чем заключается применение ряда Тейлора для численного дифференцирования?
Практическое занятие № 17
Тема: «Численное решение обыкновенных дифференциальных уравнений. Метод Эйлера»
Основные вопросы: Задача Коши. Существование и единственность решения задачи Коши. Геометрический смысл правой части дифференциального уравнения. Понятие численного решения задачи Коши. Метод Эйлера. Усовершенствования метода Эйлера. Метод Эйлера-Коши. Метод Рунге-Кутты. Учет погрешностей квадратурных формул методом двойного перерасчета.
Краткие теоретические сведения: Пусть требуется найти на отрезке [ а, b ] решение обыкновенного дифференциального уравнения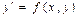 
при заданном начальном условии 
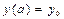. Решением дифференциального уравнения называется такая дифференцируемая функция 
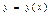, которая при подстановке в уравнение обращает его в тождество.
Рассмотрим численные методы решения этой задачи. Отметим, что численные методы дают искомое приближенное решение в виде таблицы значений.
Разобьем отрезок [ а, b ] на n равных частей - элементарных отрезков точками x 0, x 1,..., хn, причем, х 0 = а, хn = b. Величину 
будем называть шагом интегрирования. Тогда
.
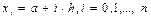Метод Эйлера. Согласно методу Эйлера, зная значение искомой функции в начале отрезка [ а, b ]: 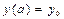, приближенное значение решения уравнения в точке у1, можно определить по формуле
.
Затем в качестве у0 выступает значение у1, находится у2 и т.д.
Общая итерационная формула метода Эйлера имеет вид
.
Геометрический смысл метода Эйлера заключается в аппроксимации решения на отрезке [ xi, xi+1 ] отрезком касательной, проведенной к графику решения в точке xi (рис. 20). Затем строится касательная к кривой у = у (х) в точке xi+1 и переносится параллельно самой себе до совмещения с концом касательной, полученной на предыдущей итерации.
Полученная ломаная и будет представлять собой приближенное решение, полученное методом Эйлера.
Формула Эйлера имеет погрешность метода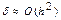 
.
Часто при решении дифференциального уравнения численными методами требуется обеспечить точность вычислений ɛ. Для практического выбора шага h с целью обеспечения заданной точности ɛ применяется следующий прием.
Выполняются два расчета: с числом разбиений n и 2 n. Вычисления заканчивают, если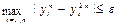 
. В случае, если полученные результаты отличаются более чем на требуемую точность, число разбиений удваивается и вновь производится сравнение результатов.
Метод Эйлера-Коши. В данном методе на каждом интервале расчет проводится в два этапа. На первом (этап прогноза) определяется приближенное решение на правом конце интервала по методу Эйлера, на втором (этапе коррекции) уточняется значение решения на правом конце с использованием полусуммы тангенсов углов наклона на концах интервала:
Dyi= 
× (f(xi, yi)+f(xi+1,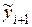 
)), где 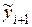= yi+h× f(xi, yi).
Абсолютную погрешность метода определяют из приближенного равенства
| 
-y(xi) |» 
| - yi |, i=1,2,…,n.
