Интерполяционный многочлен Лагранжа 2 страница

Следовательно разложение имеет вид

.

 

Порядок выполнения работы

1. Разложить в ряд Фурье функцию f (х)= х, заданную в промежутке .

2. Разложить в ряд Фурье периодическую функцию f (х) =│ x │, на отрезке .

3. Разложите в ряд Фурье только по синусам функцию , заданную в промежутке .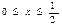

4. .

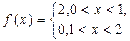5.

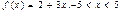
6.

7.

8.

 

Ответы: 1) .

2)

3) .

4)

5)

6)

7)

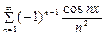
8)

Контрольные вопросы

1. Функция разложена в ряд Фурье по синусам на отрезке [0; 1]. Чему равна сумма ряда в точках ? Чему равен период суммы ряда?

 

Практическая работа № 4

 

Тема «Разложение в ряд Фурье непериодических функций»

Основные вопросы: Представление непериодической функции в ряд Фурье на любом конечном промежутке. Понятие суммы ряда во всех точках отрезка, в точке разрыва. Доопределение функции на отрезке, получение периодической функции(четным и нечетным образом).

Краткие теоретические сведения: Пусть функция f(x) задана на отрезке [ a; b ], причем функции f(x), непрерывны на [ a; b ] или имеют на этом отрезке конечное число точек разрыва первого рода. Покажем, что заданную функцию f(x) в точках ее непрерывности можно представить в виде суммы ряда Фурье.

 

 

Рисунок 7

 

Для этого рассмотрим функцию f₁(x) с периодом , совпадающую с функцией f(x) на отрезке [ a; b ]. Разложим функцию f₁(x) в ряд Фурье

Если 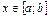, то f₁(x) = f(x), следовательно,

 

.

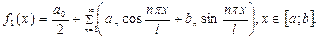Это и есть разложение в ряд Фурье функции f(x), заданной на отрезке [ a; b ].

Рассмотрим два частных случая.

1. Пусть функция f(x) задана на отрезке [ 0; l ]. Доопределим так, чтобы при 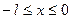было f(x) = f(-x), в результате получится четная функция

.

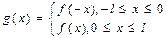В этом случае говорят, что функция f(x) продолжена четным образом

Разложим функцию g (x) на отрезке [- l; l ] в ряд Фурье

где

Коэффициенты , так как g (х) – четная функция.

Если , то g (x) и f(x), следовательно,

2. Аналогично, продолжая f(x) нечетным образом, получим нечетную функцию

 

 

Рисунок 8

,

которая разлагается в ряд Фурье по синусам.

На отрезке [0; l ]

где .

Таким образом, функцию f(x), заданную на отрезке [0; l ], можно разложить в ряд Фурье как по косинусам, так и по синусам.

Примеры решения задач

Пример 1. Пусть требуется разложить функцию f(x) = x на отрезке [0; 1] в ряд по косинусам.

Решение. Продолжим эту функцию четным образом, получим , . Разлагая ее в ряд, найдем

При будем иметь

Пример 2. Разложить функцию f(x) = x на отрезке [0; 1] в ряд Фурье по синусам.

Решение. Искомое разложение имеет вид ,

где . Так как l =1, а f(x) = x , то

.

следовательно,

Пример 3. Разложить в ряд Фурье 2 l -периодическую функцию , на .Построить график суммы ряда.

Решение. Для вычисления коэффициентов Фурье воспользуемся формулами

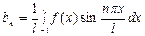, , , n =0, 1, 2, ….

Имеем: .

 

n =0, 1, 2, 3, ….

Аналогично находим

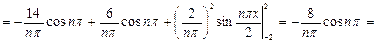
Подставляя найденные коэффициенты в формулу, получаем разложение функции f(x) в ряд Фурье: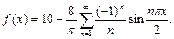

Построим график суммы ряда. Сумма ряда S(x) имеем период Т =2 l =4 и S(x) = f(x), т. е. для всех

Если ,

 

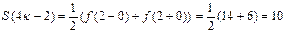
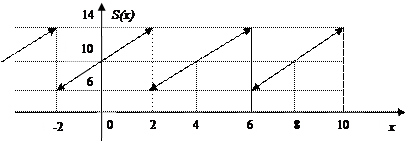
Рисунок 9

Порядок выполнения работы

1. Разложите в ряд Фурье периодическую функцию, заданную в промежутке :

а) б)

в) г)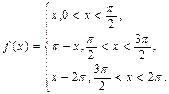

Ответ: а) .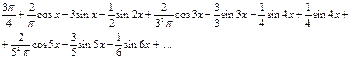

б) .

в) .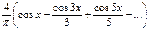

г) .

Контрольные вопросы

1. Сформулируйте правила разложения функций в ряд Фурье, заданных на промежутке [0; 2 l ].

Практическая работа № 5

Тема: «Комплексная форма рядов Фурье»

Основные вопросы: Разложение периодических кривых геометрически правильной формы и кривых произвольной (геометрически правильной) формы.

Краткие теоретические сведения: Пусть функция f (x) определена . Применяя формулы Эйлера , , .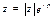

Можно записать в ряд Фурье данной функции в комплексной форме:

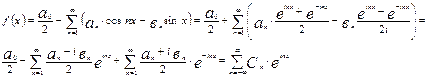
Мы использовали здесь следующие обозначения

, , .

Коэффициенты С n называется комплексными коэффициентами Фурье.

Они определяются формулами

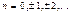
Если нужно построить продолжение функции f(x),имеющей произвольный период 2L,то соответствующее выражение в комплексной форме имеет вид

где, ,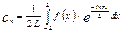

Комплексная форма ряда Фурье алгебраически проще и более симметрична. Поэтому, она часто используется в физике и прикладных расчетах.

Примеры решения задач

Пример 1. Используя комплексную форму записи, найти разложение в ряд Фурье функции.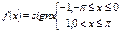

Решение: Вычислим коэффициент С₀ и С_n ().

Если n =2 k, то С_2k=0

Если n = 2 k-1, то

Следовательно, разложение в ряд Фурье в комплексной форме имеет вид:

Данный ряд можно преобразовать и записать в действительных переменных. Обозначим:

n = 2 k-1, тогда

Контрольные вопросы

1. Выведите формулы для коэффициентов Фурье для функции комплексного переменного.

 

Практическая работа № 6

Тема: «Разложение функций в ряд Фурье

для анализа несинусоидальных напряжений и токов»

Основные вопросы: Разложение периодических кривых геометрически правильной формы и кривых произвольной (геометрически правильной) формы.

Краткие теоретические сведения: При изучении различных зависимостей в электических цепях с несинусоидальными токами применяют ряды Фурье. Переменный синосоидальный ток имеет период . Несинусоидальный ток разлагают в ряд Фурье вида

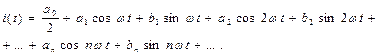(9)

Формулы для нахождения коэффициентов ряда (9) получаются из формул:

, , ,

 

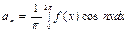с помощью замены переменной и имеют вид:

, , . (10)

Примеры решения задач

Пример 1. Разложить в ряд Фурье функцию двухполупериодного выпрямленного синусоидального тока:

.

Решение:

 

 

Рисунок 10

Данная функция является четной, поэтому . По формулам (2) находим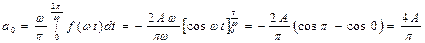

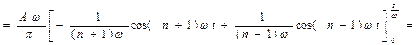
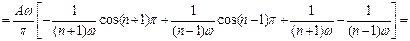
Тогда , ,

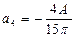Подставляя эти значения в (1), получим

или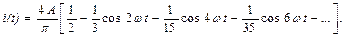

Пример 2. Разложить в ряд Фурье функцию

Решение. Выполним рисунок функции

 

 

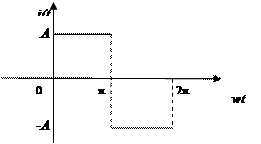
Рисунок 11

 

Данная функция является нечетной, поэтому . По формулам (2) находим

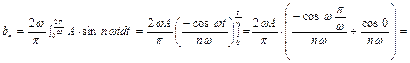
при ,

при ,

при ,

при .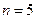

Пример 3. Разложите в ряд Фурье функцию .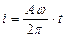

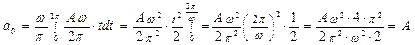
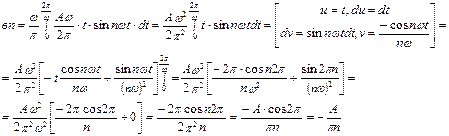
Порядок выполнения работы

 

1. Разложите в ряд Фурье функцию однополупериодного выпрямленного синусоидального тока (рисунок 12).

 

Рисунок 12

2. Разложите в ряд Фурье функцию двухполупериодного выпрямленного синусоидального тока (рисунок 13).

 

 

Рисунок 13

 

Ответы: 1)

2)

Контрольные вопросы

1. Каковы основные свойства функций, образующих основную тригонометрическую систему?

2. Можно ли функцию разложить в ряд Фурье на отрезке .

3. Функция разложена в ряд Фурье на отрезке . Чему равна сумма ряда в точках х = 0, х = –π?

4. По каким функциям разлагается в ряд Фурье четная (нечетная) функция?

5. Функция разложена в ряд Фурье по синусам на отрезке . Чему равна сумма ряда в точках ? Чему равен период суммы ряда?

6. Сформулируйте определение ряда и коэффициентов Фурье.

7. Сформулируйте теорему о сходимости ряда Фурье.

8. Запишите разложение функции с произвольным периодом в ряд Фурье.

Практическая работа № 7

Тема: «Погрешности приближенных значений чисел»

Основные вопросы: Абсолютная и относительные погрешности. Значащие и верные цифры. Действия над приближенными цифрами.

Краткие теоретические сведения:

Определение 1: Модуль разности между точным значением х и его приближенным значением а называется абсолютной погрешностью приближенного значения х и обозначается :

, .

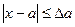Пример 1. Даны приближенные значения числа . Какое из этих трех приближений является лучшим?

Решение. Найдем абсолютную погрешность каждого числа

; ; .

Лучшим приближением числа х является .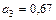

Определение 2. Цифра m приближенного числа а называется верной в широком смысле, если граница абсолютной погрешности числа а не превосходит единицы того разряда, в котором записывается цифра m.

Определение 3. Цифра m приближенного числа а называется верной в строгом смысле, если граница абсолютной погрешности числа а не превосходит половины единицы того разряда, в котором записана цифра m.

В числах, полученных в результате измерений или вычислений и используемых при расчетах в качестве исходных данных, а также в десятичной записи приближенного значения, все цифры должны быть верными.

Цифры в записи приближенного числа, о которых не известно, являются ли они верными, называются сомнительными.

Значащими цифрами приближенного числа называются все его верные цифры, кроме нулей, стоящих перед первой цифрой.

Пример 2. Указать верные цифры (в строгом смысле) следующего числа .

Решение. Начнем проверку

«1» относится к разряду десятки, 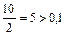, следовательно 1 – цифра верная;

«2» относится к разряду единиц, , следовательно 2 – цифра верная;

«3» относится к разряду десятых, , следовательно 3 – цифра неверная.

Таким образом число 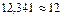с точностью до 0,1.

Пример 3. Число округлить до первоговерного разряда.

Решение. Так как цифры «9» и «5» верные, то .

Определение 4: Относительной погрешностью приближеного значения а числа х называется отношение абсолютной погрешности 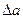этого приближения к числу а, т.е. .

Пример 4. Найти относительную погрешность числа 6,8, если обе цифры его верные.

Решение. По условию , поэтому .

Действия над приближенными числами

Функция	Граница абсолютной погрешности	Граница относительной погрешности

 

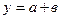
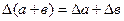
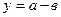
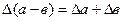
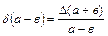
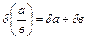
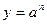
Примеры решения задач

Пример 5. Найдите относительную погрешность вычисления площади прямоугольника со сторонами и .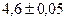

Решение. ,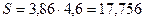

Пример 6. С какой точностью надо измерить радиус круга, чтобы абсолютная погрешность площади круга не превышала ? Грубое приближенное значение R = 8,7 см.

Решение. Площадь круга равна . Абсолютная погрешность площади равна , . Следовательно, если измерить величину R с погрешностью, не превышающей 0,2 см, то погрешность площади не превысит .

Порядок выполнения работы

1. Найдите относительную погрешность равенства .

2. Число 8,75 найдено с относительной погрешностью 0,4%. Определите границу абсолютной погрешности.

3. Найдите относительную погрешность вычисления площади прямоугольника со сторонами и .

4. Найдите относительную погрешность вычисления объема прямоугольного параллелепипеда с измерениями , и 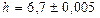.