Dyi=  , где
, где

Абсолютная погрешность находится с помощью равенства
|  -y(xi) |»
-y(xi) |»  |
|  - yi |, i=1,2,…,n
- yi |, i=1,2,…,n
Примеры решения задач
Методом Эйлера проинтегрировать задачу Коши на отрезке  с шагом
с шагом  и шагом
и шагом  . Оценить погрешность
. Оценить погрешность
 ,
, 
Решение: В точках  ,
,  значение искомой интегральной кривой вычисляются по формулам:
значение искомой интегральной кривой вычисляются по формулам:

При пересчете значений интегральной кривой с удвоенным шагом воспользуемся уже вычисленными значениями 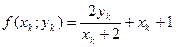
Результаты вычислений приводятся в следующей таблице:
| k | 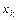 (1) (1)
|  (2)
(2)
|  (3) (3)
|  (4) (4)
|  (5)
(5)
|  (6) (6)
|
| 0,1 | 1,25 | 2,29048 | 0,11452 | 1,25 | 0,22904 | |
| 0,15 | 1,36452 | 2,41932 | 0,12096 | |||
| 0,2 | 1,48548 | 2,55043 | 0,12752 | 1,47904 | 0,25504 | |
| 0,25 | 1,613 | 2,68378 | 0,13418 | |||
| 0,3 | 1,74718 | 2,81928 | 0,14096 | 1,73408 | 0,28192 | |
| 0,35 | 1,88814 | 2,95692 | 0,14784 | |||
| 0,4 | 2,03598 | 3,09665 | 0,15483 | 2,016 | 0,30966 |
Ответ:
| 0,1 | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 |
| 1,25 | 1,36 | 1,49 | 1,61 | 1,75 | 1,89 | 2,04 |
Пример 2. Решить дифференциальное уравнение  с начальными условиями у(0)=0 на интервале [0; 0,5]методом Эйлера-Коши.
с начальными условиями у(0)=0 на интервале [0; 0,5]методом Эйлера-Коши.
Решение. Исходя из начальных значений x0=0, y0=0, рассчитаем значение y1 в узле x1=0,1 по формулам:

Аналогично получим решение в остальных узлах. Продолжим вычисления и, введя обозначение 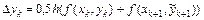 , получаемые результаты занесем в таблицу.
, получаемые результаты занесем в таблицу.

| 
| 
| 
| 
| 
| 
|
| 0,0 0,1 0,2 0,3 0,4 0,5 | 0,000000000 0,000000000 0,003035327 0,009813786 0,023408346 0,047024301 | 0,00000 1,510025E-003 7,157661E-003 1,941224E-002 4,133581E-002 | 0,000500000 0,002535327 0,006778459 0,013594561 0,023615954 | 0,000000000 0,000334672 0,002710036 0,009336250 0,022793219 0,046302490 | 0,000000000 0,1653E-03 0,3253E-03 0,4775E-03 0,6151E-03 0,7218E-03 |
Решением задачи является табличная функция (оставлены 5 значащих цифр в каждом числе).

| ||||||
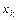

| 0,00000 0,00000 | 0,100000 0,000500 | 0,2000000 0,0030353 | 0,300000 0,0098138 | 0,400000 0,023408 | 0,500000 0,047024 |
Пример 3. Решить дифференциальное уравнение  с начальными условиями у(0)=0 на интервале [0; 0,5]методом Рунге – Кутты четвертого порядка.
с начальными условиями у(0)=0 на интервале [0; 0,5]методом Рунге – Кутты четвертого порядка.
Решение. Вычислим значения вспомогательных величин:

Найдем приращение функции на первом интервале

и значение функции в первом узле

Аналогично получим решение в остальных узлах, результат занесем в таблицу:

| 
| 
| 
| 
| 
| 
| 
|
| 0/1 0/2 0/3 0/4 | 0,0 0,05 0,05 | 0,0000000 0,0000000 0,0001250 0,00025125 | 0,000000000 0,000250000 0,000251252 0,001005031 | 0,000334589 | 0,005006 | 0,000000 | 0,000000000 |
| 1/1 1/2 1/3 1/4 | 0,1 0,15 0,15 0,2 | 0,000334589 0,000837941 0,001472193 0,002628972 | 0,001006703 0,002275208 0,002294383 0,004105850 | 0,002375289 | 0,015116 | 0,00033467 | 0,8301E-07 |
| 2/1 2/2 2/3 2/4 | 0,2 0,25 0,25 0,3 | 0,002709878 0,004764443 0,005955124 0,009261181 | 0,004109129 0,006490492 0,006551303 0,009564248 | 0,006626161 | 0,025535 | 0,002710036 | 0,1573E-06 |
| 3/1 3/2 3/3 ¾ | 0,3 0,35 0,35 0,4 | 0,009336039 0,014120479 0,015965225 0,022729094 | 0,009568879 0,013258372 0,013393055 0,017869989 | 0,013456954 | 0,036504 | 0,009336250 | 0,2103E-06 |
| 4/1 4/2 4/3 4/4 | 0,4 0,45 0,45 0,5 | 0,022792993 0,031730689 0,034396216 0,046256962 | 0,017875391 0,023206446 0,023463969 0,029839667 | 0,023509315 | 0,048306 | 0,022793219 | 0,2259E-06 |
| 0,5 | 0,046302308 | 0,046302490 | 0,1823E-06 |
Решение задачи является табличная функция – таблица 4.8 (оставлены 7 значимых цифр в каждом числе).

| ||||||
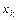

| 0,00000 0,00000 | 0,10000 0,000334589 | 0,200000 0,002709878 | 0,300000 0,009336039 | 0,400000 0,02279299 | 0,500000 0,04630231 |
Порядок выполнения работы: Дано дифференциальное уравнение  с начальным условием
с начальным условием  . Приняв шаг интегрирования h = 0,1, выполнить две итерации с помощью:
. Приняв шаг интегрирования h = 0,1, выполнить две итерации с помощью:
1) метода Эйлера;
2) исправленного метола Эйлера;
3) метода Рунге-Кутта четвертого порядка точности;
4) сравнить результаты, полученные в точке х = 0,2, с точным решением (найти его самостоятельно), определить абсолютную и относительную погрешности каждого метода.
Контрольные вопросы
1. Итерационная формула метода Эйлера.
2. Итерационная формула исправленного метода Эйлера.
3. Итерационная формула метода Рунге-Кутга четвертого порядка точности.
Практическое занятие № 18
Тема: « Численные методы решения систем линейных уравнений. Методы Гаусса»
Основные вопросы: Способы определения расстояния в пространстве Rn. Абсолютная погрешность числового вектора и его координат. Сходимость последовательности векторов в Rn. Приведенная система уравнений, способы преобразования систем к приведенному виду. Построение итерационной последовательности. Достаточное условие сходимости итерационной последовательности. Оценка погрешности итерационного решения. Условие окончания итерационного процесса при нахождении решения с заданной точностью.
Краткие теоретические сведения: При решении методом Гаусса матрица СЛАУ с помощью равносильных преобразований превращается в верхнюю треугольную матрицу в результате прямого хода. В обратном ходе определяются неизвестные.
Пусть дана СЛАУ

Выпишем расширенную матрицу системы:



 На первом шаге алгоритма Гаусса выберем диагональный элемент
На первом шаге алгоритма Гаусса выберем диагональный элемент  (если он равен нулю, то первую строку переставляем в какой-либо нижележащей строкой) и объявляем его ведущим, а соответствующую строку и столбец, на пересечении которых он стоит, - ведущими. Обнулим элементы
(если он равен нулю, то первую строку переставляем в какой-либо нижележащей строкой) и объявляем его ведущим, а соответствующую строку и столбец, на пересечении которых он стоит, - ведущими. Обнулим элементы  ведущего столбца. Для этого сформируем числа
ведущего столбца. Для этого сформируем числа 
Умножая ведущую строку на число  складывая со второй и ставят на место второй строки, получим вместо элемента
складывая со второй и ставят на место второй строки, получим вместо элемента  нуль, а вместо элементов
нуль, а вместо элементов  соответственно элементы
соответственно элементы

и т.д.
Умножая ведущую строку на число  складывая с n-й строкой и ставя результат на местоn-й строки, получим вместо элемента
складывая с n-й строкой и ставя результат на местоn-й строки, получим вместо элемента  нуль, а остальные элементы этой строки будут иметь вид
нуль, а остальные элементы этой строки будут иметь вид

Сохраняя ведущую строку неизменной, получим в результате первого шага алгоритма Гаусса следующую матрицу:

На втором шаге алгоритма Гаусса в качестве ведущего элемента выбирается элемент  (если он равен нулю, то вторую строку взаимно меняем на нижележащую строку). Формируются следующие числа:
(если он равен нулю, то вторую строку взаимно меняем на нижележащую строку). Формируются следующие числа:  Умножая ведущую строку на число
Умножая ведущую строку на число 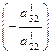 и складывая результаты с третьей строкой, получим вместо элемента
и складывая результаты с третьей строкой, получим вместо элемента  нуль, а вместо элементов
нуль, а вместо элементов  элементы
элементы  и т.д. Умножая ведущую строку на число
и т.д. Умножая ведущую строку на число  складывая результат сn-й строкой и ставя полученную сумму на место n-й строки, получим вместо элемента
складывая результат сn-й строкой и ставя полученную сумму на место n-й строки, получим вместо элемента  нуль, а вместо элементов
нуль, а вместо элементов  соответственно элементы
соответственно элементы 
Сохраняя первую и вторую строки матрицы неизменными, получим в результате второго шага алгоритма Гаусса следующую матрицу:

После (n-1)-го шага алгоритма Гаусса получаем следующую расширенную матрицу, содержащую верхнюю треугольную матрицу СЛАУ:

Прямой ход алгоритма Гаусса завершен.
В обратном ходе алгоритма Гаусса из последнего уравнения сразу определяется 
из последнего -  и т.д. Из первого уравнения определяется
и т.д. Из первого уравнения определяется  :
:

Замечание 1. Если элементы какой-либо строки матрицы системы в результате преобразований стали равными нулю, а правая часть не равна нулю, то СЛАУ несовместна, поскольку не выполняются условия теоремы Кронекера-Капелли.
Замечание 2. Если элементы какой-либо строки матрицы системы и правая часть в результате преобразований стали равными нулю, то СЛАУ совместна, но имеет бесконечное множество решений, получающиеся с помощью метода Гаусса для СЛАУ порядка r, где r-ранг матрицы исходной СЛАУ.
Замечание 3. В результате прямого хода метода Гаусса можно вычислить определитель матрицы А исходной СЛАУ:

При этом с помощью множителя  , где р-число перестановок строк в процессе прямого хода, учитываются соответствующие перемены знаков вследствие перестановок строк.
, где р-число перестановок строк в процессе прямого хода, учитываются соответствующие перемены знаков вследствие перестановок строк.
Замечание 4. Метод Гаусса можно применить для обращения невырожденной  матрицы.
матрицы.
Действительно, пусть требуется обратить невырожденную матрицу  Тогда, обозначив
Тогда, обозначив  можно выписать матричное уравнение АХ=Е, где
можно выписать матричное уравнение АХ=Е, где
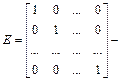
Единичная матрица, и его основе записать цепочку СЛАУ

каждую из которых можно решить методом Гаусса. При этом, поскольку верхняя треугольная матрица для всех СЛАУ будет одной и той же, прямой ход метода Гаусса применяется лишь один раз. Строится следующая расширенная матрица:

В результате применения (n-1)-го шага метода Гаусса получаем:

При этом первый столбец  обратной матрицы определяется в обратном ходе метода Гаусса с правой частью
обратной матрицы определяется в обратном ходе метода Гаусса с правой частью  второй столбец
второй столбец  с правой частью
с правой частью  и т.д. Столбец
и т.д. Столбец  определяется с правой частью
определяется с правой частью 
Примеры решения задач: Методом Гаусса решить СЛАУ

Решение. Прямой ход:



Обратный ход:

Ответ: 
Порядок выполнения работы: Методом Гаусса решить системы линейных алгебраических уравнений (СЛАУ). Для матрицы СЛАУ вычислить определитель и обратную матрицу.
1.  2.
2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
Ответы
1. 
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 






