1. Написать уравнение плоскости, проходящей через точку М(2,4,-3) перпендикулярно прямой  (рис.11).
(рис.11).
Решение:
 {5;-1;2} {5;-1;2}
|
| М(2;4;-3) |
| Рис. 11 |
Чтобы написать уравнение плоскости A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0, необходимо знать координаты любой точки, лежащей в плоскости (у нас это точка М(2;4;-3)), и координаты вектора, перпендикулярного плоскости. Так как прямая  перпендикулярна плоскости, то ее направляющий вектор
перпендикулярна плоскости, то ее направляющий вектор  {5;-1;2} можно взять в качестве вектора-нормали к плоскости. Теперь запишем уравнение искомой плоскости:
{5;-1;2} можно взять в качестве вектора-нормали к плоскости. Теперь запишем уравнение искомой плоскости:
5(х -2)-1(у -4)+2(z +3)=0;
5 х- 10- у +4+2 z +6=0;
5 х - у+ 2 z =0.
Ответ: 5 х-у+ 2 z =0.
2. Написать канонические уравнения прямой, проходящей через точку М(2;4;-3) перпендикулярно плоскости 3 х- 2 у+ 5 z -1=0 (рис.12).
Решение:
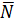 {-3;-2;5} {-3;-2;5}
|
| М(2;4;-3) |
| Рис.12 |
Чтобы написать канонические уравнения прямой в пространстве  , необходимо знать координаты любой точки М(х 0, у 0, z 0), через которую проходит прямая (у нас эта точка М(2;4;-3)), и координаты направляющего вектора
, необходимо знать координаты любой точки М(х 0, у 0, z 0), через которую проходит прямая (у нас эта точка М(2;4;-3)), и координаты направляющего вектора  { m; n; p }(вектора, параллельного прямой). Так как прямая перпендикулярна плоскости, то она параллельна вектору нормали к плоскости. Следовательно, определив из уравнения плоскости координаты вектора нормали
{ m; n; p }(вектора, параллельного прямой). Так как прямая перпендикулярна плоскости, то она параллельна вектору нормали к плоскости. Следовательно, определив из уравнения плоскости координаты вектора нормали  {-3;-2;5}, возьмем его в качестве направляющего вектора прямой. Теперь запишем каноническое уравнение искомой прямой
{-3;-2;5}, возьмем его в качестве направляющего вектора прямой. Теперь запишем каноническое уравнение искомой прямой
 .
.
Ответ:  .
.
3. Написать уравнения прямой, проходящей через точку М0(2;-3;-4) параллельно прямой 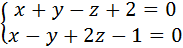 .
.
Решение:
Уравнение прямой будем искать в виде  , где
, где
x 0, y 0, z 0 – координаты точки, через которую проходит прямая (у нас это точка М0(2;-3;-4)),  { m; n; p } – направляющий вектор прямой. Так как искомая прямая параллельна заданной прямой, у них один и тот же направляющий вектор. Найдем направляющий вектор прямой, заданной в условии общими уравнениями. Общие уравнения прямой задают, как линию пересечения двух плоскостей (рис.13).
{ m; n; p } – направляющий вектор прямой. Так как искомая прямая параллельна заданной прямой, у них один и тот же направляющий вектор. Найдем направляющий вектор прямой, заданной в условии общими уравнениями. Общие уравнения прямой задают, как линию пересечения двух плоскостей (рис.13).

|

|

|

|

|
| М0(2;-3;-4) |
| Рис.13 |
Из общих уравнений плоскостей определяем координаты их нормалей  {1;1;-1} и
{1;1;-1} и 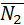 {1;-1;2}. Заметим, что направляющий вектор
{1;-1;2}. Заметим, что направляющий вектор  ^
^  и
и  ^
^  , следовательно, вектор
, следовательно, вектор  можно найти как векторное произведение
можно найти как векторное произведение  и
и 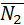 .
.
 ´
´ 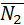 =
= 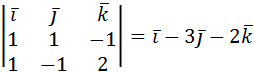 .
.
 {1;-3;-2} – направляющий вектор искомой прямой. Тогда канонические уравнения прямой имеют вид:
{1;-3;-2} – направляющий вектор искомой прямой. Тогда канонические уравнения прямой имеют вид:  .
.
Ответ:  .
.
4. Написать уравнение плоскости, проходящей через пару параллельных прямых  и
и  (рис. 14).
(рис. 14).
Решение:
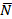
|

|

|

|

|

|
| Рис.14 |
Чтобы написать уравнение плоскости в виде A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0, необходимо знать координаты любой точки М0(x 0, y 0, z 0), лежащей в плоскости, и координаты вектора  {А,В,С}, перпендикулярного плоскости.
{А,В,С}, перпендикулярного плоскости.
Из уравнений прямых определяем координаты точек М1(2;1;0) и М2(-1;1;3), лежащих на прямых, а следовательно, и в искомой плоскости. В качестве М0(x 0, y 0, z 0) можем взять любую из них.
Теперь ищем вектор нормали. Заметим, что направляющий вектор прямых  {4;-2;1} параллелен плоскости, а следовательно,
{4;-2;1} параллелен плоскости, а следовательно,  ^
^  . Вектор
. Вектор  лежит в плоскости, следовательно,
лежит в плоскости, следовательно, 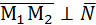 . Тогда
. Тогда  =
=  .
.
 ={-1-2;1-1;3-0}={-3;0;3}.
={-1-2;1-1;3-0}={-3;0;3}.
 =
=  =
=  .
.
Итак,  {-6;-15;-6} – нормальный вектор плоскости. Подставим координаты вектора и координаты любой из точек М1 или М2 в уравнение плоскости A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0, получим: -6(х -2)- -15(у -1)-6(z -0)=0 (мы подставили точку М1(2;1;0)).
{-6;-15;-6} – нормальный вектор плоскости. Подставим координаты вектора и координаты любой из точек М1 или М2 в уравнение плоскости A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0, получим: -6(х -2)- -15(у -1)-6(z -0)=0 (мы подставили точку М1(2;1;0)).
2(х -2)+5(у -1)+2(z -0)=0;
2 х -4+5 у -5+2 z =0;
2 х +5 у +2 z -9=0.
Ответ: 2 х +5 у +2 z -9=0.
5. Написать уравнение плоскости, проходящей через точки М1(-1;0;2) и М2(3;2;1) перпендикулярно плоскости α: 2 х -3 у + z -5=0.
Решение:

|

|

|

|
|

|
| Рис.15 |
Ищем уравнение плоскости β в виде A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0 (рис.15). Нам необходимо иметь координаты любой точки, лежащей в плоскости (у нас их две М1 и М2), и координаты вектора нормали. Так как вектора нормали  в условии задачи нет, следует найти любые два вектора, ортогональные нормали. Тогда их векторное произведение даст нам нормаль. На рис.15 видно, что
в условии задачи нет, следует найти любые два вектора, ортогональные нормали. Тогда их векторное произведение даст нам нормаль. На рис.15 видно, что  и
и 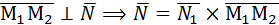 . Координаты вектора
. Координаты вектора  {2;-3;1}определяются из уравнения плоскости α. Найдем координаты вектора
{2;-3;1}определяются из уравнения плоскости α. Найдем координаты вектора  .
.
 ={3-(-1);2-0;1-2}={4;2;-1}.
={3-(-1);2-0;1-2}={4;2;-1}.
 =
=  .
.
Подставляем координаты вектора  {1;6;16} и координаты любой из точек М1 и М2 (мы возьмем М1(-1;0;2)) в уравнение плоскости, получим:
{1;6;16} и координаты любой из точек М1 и М2 (мы возьмем М1(-1;0;2)) в уравнение плоскости, получим:
1(х +1)+6(у -0)+16(z -2)=0;
х +6 у +16 z -31=0;
Ответ: х +6 у +16 z -31=0.
6. Написать уравнение плоскости, проходящей через прямую  и точку М(2;3;-4).
и точку М(2;3;-4).
|
| М1(1;0;-2) |

|
| М(2;3;-4) |
| Рис.16 |
Чтобы написать уравнение плоскости A (x-x 0 )+ B (y-y 0 )+ C (z-z 0 ) =0, необходимо знать координаты точки, лежащей в плоскости (у нас точка М(2;3;-4)), и координаты вектора нормали  .
.
В условии задачи нет вектора нормали, но мы заметим (рис. 16), что направляющий вектор прямой  {2;-1;3}^
{2;-1;3}^  и вектор
и вектор  . Тогда
. Тогда  . Определив из уравнений прямой координаты точки М1(1;0;-2), найдем вектор
. Определив из уравнений прямой координаты точки М1(1;0;-2), найдем вектор  ={1-2;0-3;-2-(-4)}={-1;-3;2}.
={1-2;0-3;-2-(-4)}={-1;-3;2}.
 =
=  . Теперь запишем уравнение искомой плоскости:
. Теперь запишем уравнение искомой плоскости:
7(х -2)-7(у -3)-7(z +4)=0;
7 х -14-7 у +21-7 z -28=0;
7 х -7 у -7 z -21=0;
х - у - z -3=0.
Ответ: х - у - z -3=0.




