1. Найти длину вектора 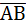 , если А(1;2;3); В(2;-5;4).
, если А(1;2;3); В(2;-5;4).
Решение:
Найдем координаты вектора 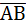 :
: 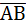 {2-1;-5-2;4-3}; АВ{1;-7;1}.
{2-1;-5-2;4-3}; АВ{1;-7;1}.
Найдем длину вектора 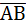 :
:
 .
.
Ответ:  .
.
2. Найти длину радиус-вектора точки А(2;3;-1).
Решение:
Координаты радиус-вектора точки А совпадают с координатами самой точки:  {2;3;-1}.
{2;3;-1}.
Найдем длину радиус-вектора  :
:
 .
.
Ответ: 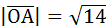 .
.
3. Найти длину вектора  , если
, если  {1;-1;0},
{1;-1;0}, 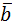 {3;-1;4}.
{3;-1;4}.
Решение:
Найдем координаты вектора  :
:  {1+3∙3;-1+3(-1);0+3∙4};
{1+3∙3;-1+3(-1);0+3∙4};  {10;-4;12}.
{10;-4;12}.
Найдем длину вектора  :
:
 .
.
Ответ:  =
=  .
.
4. Найти направляющие косинусы вектора 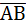 , если А(1;-1;3), В(2;-3;4).
, если А(1;-1;3), В(2;-3;4).
Решение:
Найдем координаты вектора 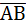 :
: 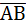 {2-1;-3-(-1);4-3},
{2-1;-3-(-1);4-3}, 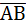 {1;-2;1}.
{1;-2;1}.
Найдем длину вектора 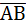 :
:
 .
.
Итак,  ;
;  ;
;  .
.
Проверка:  .
.
Ответ:  ;
;  ;
;  .
.
Скалярное произведение двух векторов
| Свойства |
| Определение |
| Применение |
Скалярным произведением двух векторов называется число, равное произведению длин векторов на косинус угла между ними: 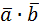 =| =|  || || 
|
 |
| 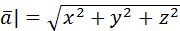
|
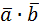 = = 
|

k (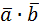 )=
= (k )=
= (k 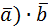 =
= =
=  ) )
|
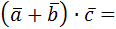

|

|



|


|


|
Работа силы F на перемещение S А= 
|
Вычисление в прямоугольных координатах: если

 , то , то
 . .
|
Скалярное произведение ортов
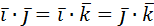 =0 =0
 =1 =1
|
Примеры решения типовых задач
1. Даны векторы  =3
=3  и
и  . Найти: а)
. Найти: а) 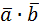 ;
;
б)  ; в)
; в)  .
.
Решение:
а) 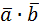 =3∙2+(-1)3+2(-1)=6-3-2=1;
=3∙2+(-1)3+2(-1)=6-3-2=1;
б)  ;
;
в)  .
.
Ответ: а) 1; б)  ; в)
; в)  .
.
2. Даны векторы  {3;-1;4},
{3;-1;4}, 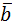 {-2;2;2}. Проверить, являются ли они ортогональными.
{-2;2;2}. Проверить, являются ли они ортогональными.
Решение:
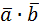 =3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы
=3∙(-2)+(-1)2+4∙2=-6-2+8=0. Следовательно, векторы  ортогональны.
ортогональны.
3. Вычислить работу силы  ={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
={3;2;4}, если точка ее приложения перемещается прямолинейно из положения А(2;4;6) в положение В(4;2;7).
Решение:
А =  . Найдем координаты вектора
. Найдем координаты вектора  =
=  :
:
 {4-2;2-4;7-6};
{4-2;2-4;7-6};
 ={2;-2;1}.
={2;-2;1}.
Найдем работу А:
А=3∙2+2(-2)+4∙1=6-4+4=6.
Ответ: 6.
4. Найти длины диагоналей параллелограмма (рис.1), построенного на векторах  , где
, где  =60˚.
=60˚.

|

|


|
| Рис.1 |
Решение:
Выразим диагонали параллелограмма  и
и  по правилу
по правилу
параллелограмма:  ,
,
 .
.
Так как векторы  не единичные, следовательно,
не единичные, следовательно,  заданы в произвольном базисе, то
заданы в произвольном базисе, то  и
и  можно найти по определению:
можно найти по определению:
 =
=
 =
=  .
.
 =
=
 =
=  .
.
Ответ:  =
=  .
.
A. Векторное произведение двух векторов
| Свойства |
| Определение |
| Применение |
Площадь треугольника
S= 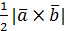
|
Векторным произведением двух векторов называется вектор  , длина которого численно равна площади параллелограмма, построенного на векторах , длина которого численно равна площади параллелограмма, построенного на векторах  и и  и направлен так, что кратчай-ший поворот от и направлен так, что кратчай-ший поворот от  к к  видится против часовой стрелки видится против часовой стрелки
|
 = = 
|

Вычисление

|
Условие коллинеарности

|
Момент силы  , в точке А относительно точки О: , в точке А относительно точки О: 
|
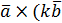 )=
= k( )=
= k(  ) )
|


|
Примеры решения типовых задач
1. Раскрыть скобки и упростить выражение:
а)  ;
;
б) (2  .
.
Решение:
а) 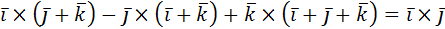 +
+ 
 =2
=2 
б) (2  =2
=2 
 .
.
2. Даны векторы  и
и 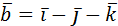 . Найти
. Найти  .
.
Решение:

 .
.
Ответ:  .
.
3. Найти площадь ∆АВС, если А(1;2;0); В(3;0;-3); С(5;2;6).
Решение:
S∆АВС=  . Найдем координаты векторов
. Найдем координаты векторов  :
:
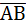 {3-1;0-2;-3-0}={2;-2;-3};
{3-1;0-2;-3-0}={2;-2;-3};
 {5-1;2-2;6-0}={4;0;6}.
{5-1;2-2;6-0}={4;0;6}.
Найдем векторное произведение  :
:

=  .
.
 .
.
S∆АВС=  .
.
Ответ:  .
.
4. Сила 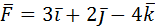 приложена в точке М(2;-1;1). Найти ее
приложена в точке М(2;-1;1). Найти ее
момент относительно начала координат.
Решение:
 . Найдем координаты вектора
. Найдем координаты вектора  : О(0;0;0), М(2;-1;1), следовательно,
: О(0;0;0), М(2;-1;1), следовательно,  {2;-1;1}.
{2;-1;1}.
 =
= 
=  .
.
Ответ:  .
.
Смешанное произведение трех векторов
| Свойства |
| Определение |
| Применение |
 = = 
|
Объем параллелепипеда
V= 
|
Смешанным произведением трех векторов называется произведение вида
( = = 
|


 , ,
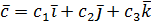 ,
то ,
то

|
Объем пирамиды
V= 
|
Условие компланарности трех векторов:
 =0 =0
|
 = =  =
= =
=  = =  = =  = = 
|

|


|






