ВЫСШАЯ МАТЕМАТИКА
ВЕКТОРНАЯ АЛГЕБРА.
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Методические указания и примеры
решения типовых задач для студентов
I курса очной формы обучения
инженерно – технических направлений
(I семестр)
Брянск 2012
УДК 511
Высшая математика. Векторная алгебра. Аналитическая геометрия. [Текс]+[Электронный ресурс]: методические указания и примеры решения типовых задач для студентов I курса очной формы обучения инженерно – технических направлений (I семестр). – Брянск: БГТУ, 2012. – 36с.
Разработали: Н.А.Ольшевская, доц.
Г.Г. Цуленева, доц.
К.А. Сенько, асс.
Рекомендовано кафедрой «Высшая математика» БГТУ
(протокол № 5 от 31.01.12)
СОДЕРЖАНИЕ
Векторная алгебра
1.1. Векторы. Основные понятия.
Линейные операции над векторами…………………………….….4
1.2. Скалярное произведение двух векторов..……………………………6
1.3. Векторное произведение двух векторов…………………………….8
1.4. Смешанное произведение трех векторов……………………..……10
1.5. Задачи для самостоятельного решения…………………………….12
Аналитическая геометрия
2.1. Прямая линия на плоскости…………………………………………13
2.2. Кривые второго порядка на плоскости……………………..………19
2.3. Плоскость в пространстве………………………………….…..……24
2.4. Прямая в пространстве. Прямая и плоскость…………….…..…….27
2.5. Задачи для самостоятельного решения……………………..………34
Список рекомендуемой литературы……………………………………..……..35
ВЕКТОРНАЯ АЛГЕБРА
Векторы. Основные понятия.
Линейные операции над векторами
Геометрический вектор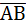 
– это направленный отрезок, у которого один конец (точка А) называется началом вектора, а другой конец (точка В) – концом вектора.
Длиной вектора (модулем) называют длину отрезка АВ. Векторы обозначают как 
, а их длины 
.
Два вектора называются равными, если они имеют равные длины и одинаковое направление.
Вектор, начало и конец которого совпадают, называется нулевым.
Произведением вектора 
на некоторое число αÎR называется вектор, длина которого равна длине вектора , умноженной на абсолютную величину числа α, а направление совпадает с направлением вектора , если α>0, и противоположно ему, если α<0.
Суммой нескольких векторов называется вектор, проведенный из начала первого вектора в конец последнего при условии, что начало каждого последующего вектора совмещается с концом предыдущего.
Проекцией вектора на ось Ох называется число, равное длине вектора , умноженной на косинус угла между вектором и положительным направлением оси Ох.
Радиусом-вектором точки М называется вектор 
соединяющий начало координат с этой точкой.
Единичные векторы координатных осей 
называются ортами.
Углы α, β, γ между вектором 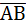и положительными направлениями осей координат называются направляющими, при этом для вектора 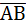с координатами Х, Y, Z
причем 
=1.
Если векторы и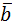 
заданы своими координатами как 
и 
, то координаты вектора 
будут равны: { ma 1 + nb 1, ma 2+ nb 2, ma 3+ nb 3}, а вектор 
ma 1 + nb 1) 
+(ma 2+ nb 2) 
+(ma 3+ nb 3) 
.
