1. Написать уравнение прямой, отсекающей на оси Оу отрезок b= -3 и составляющей с осью Ох угол 60˚.
Решение:
Воспользуемся уравнением прямой с угловым коэффициентом y=kx+b. По условию b= -3, а k = tg α= tg 60˚=Ö3. Итак, у =  х -3 – уравнение искомой прямой.
х -3 – уравнение искомой прямой.
Ответ: у =  х -3.
х -3.
2. Определить параметры k и b для каждой из прямых:
1) 3 х +4 у =12;
2) 2 х +3 у =0;
3) у =-2;
4) 
Решение:
1) 3 х +4 у =12; 2) 2 х +3 у =0; 3) y =-2; 4)  ;
;
4 у =12-3 х; 3 y =-2 x; k= 0, b= -2.  ;
;
у =  ; y =
; y =  ; y =4-
; y =4-  ;
;
y=  ; k =
; k =  , b =0. y =-
, b =0. y =-  ;
;
y= 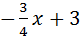 ; k =
; k =  , b =4.
, b =4.
k =  , b =3.
, b =3.
Ответ: 1) k =  , b =3; 2) k =
, b =3; 2) k =  , b =0; 3) k= 0, b= -2; 4) k =
, b =0; 3) k= 0, b= -2; 4) k =  , b =4.
, b =4.
3. Дан треугольник с вершинами А(-1;1), В(1;5), С(3;-2). Написать уравнения сторон треугольника.
Решение:
Воспользуемся способом задания прямой по 2-м точкам:
АВ:  ; BC:
; BC:  ; AC:
; AC: 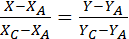 ;
;
 ;
;  ;
;  ;
;
 .
.  .
.  .
.
Ответ: АВ:  ; ВС:
; ВС:  ; АС:
; АС:  .
.
4. Дана прямая 2 х +3 у -3=0 и точка М0(1;-2). Написать уравнение прямой, проходящей через точку М0: а) параллельно заданной прямой; б) перпендикулярно заданной прямой.
Решение:
1-й способ.
а) Условие параллельности двух прямых k 1= k 2.
Пусть уравнение искомой прямой имеет вид y=k 2 x + b 2; 3 y =3-2 x; y =  ; k 1=
; k 1=  Þ k 2=
Þ k 2=  ; у =
; у = 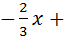 b 2. Так как М0(1;-2) принадлежит прямой, то -2=
b 2. Так как М0(1;-2) принадлежит прямой, то -2=  1+ b 2Þ b 2=-2+
1+ b 2Þ b 2=-2+  , b 2=
, b 2=  . Итак, y =
. Итак, y =  Û3 у +2 х +4=0.
Û3 у +2 х +4=0.
б) Условие перпендикулярности двух прямых k 1 k 3=-1.
Пусть уравнение искомой прямой имеет вид y=k 3 x + b 3; k 1=  Þ k 3
Þ k 3  Þ k 3=
Þ k 3=  ; y=
; y=  x + b 3. Так как М0(1;-2) принадлежит прямой, то -2=
x + b 3. Так как М0(1;-2) принадлежит прямой, то -2=  1+ b 3Þ b 3=-2
1+ b 3Þ b 3=-2  Þ b 3=
Þ b 3=  .
.
Итак,  Þ3 x -2 у -7=0.
Þ3 x -2 у -7=0.
2-й способ.
l di54bWxMj8FOwzAQRO9I/IO1SFwq6pA0bQlxKlSJCxyAwgc4yZJE2OsQu6n79ywnuM1oRrNvy120 Rsw4+cGRgttlAgKpce1AnYKP98ebLQgfNLXaOEIFZ/Swqy4vSl207kRvOB9CJ3iEfKEV9CGMhZS+ 6dFqv3QjEmefbrI6sJ062U76xOPWyDRJ1tLqgfhCr0fc99h8HY5WwdPL6+KcxvXie5PX+zhvTXz2 Rqnrq/hwDyJgDH9l+MVndKiYqXZHar0w7LOU0QOL1R0ILmRpvgJRK9hkOciqlP8/qH4AAAD//wMA UEsBAi0AFAAGAAgAAAAhALaDOJL+AAAA4QEAABMAAAAAAAAAAAAAAAAAAAAAAFtDb250ZW50X1R5 cGVzXS54bWxQSwECLQAUAAYACAAAACEAOP0h/9YAAACUAQAACwAAAAAAAAAAAAAAAAAvAQAAX3Jl bHMvLnJlbHNQSwECLQAUAAYACAAAACEAF3PNyvIBAADqAwAADgAAAAAAAAAAAAAAAAAuAgAAZHJz L2Uyb0RvYy54bWxQSwECLQAUAAYACAAAACEAdpYf698AAAAJAQAADwAAAAAAAAAAAAAAAABMBAAA ZHJzL2Rvd25yZXYueG1sUEsFBgAAAAAEAAQA8wAAAFgFAAAAAA== " strokecolor="black [3040]"/>
 . .
|
| М0(1;-2) |
| Рис.2 |
а) Из общего уравнения прямой 2 х +3 у -3=0 определяем координаты вектора нормали  . Если искомая прямая параллельна заданной, то вектор
. Если искомая прямая параллельна заданной, то вектор  будет являться нормалью и к искомой прямой (рис.2). Мы имеем нормаль и точку М0(1;-2), через которую проходит искомая прямая, поэтому используем уравнение прямой, проходящей через точку М(х 0, у 0) перпендикулярно вектору
будет являться нормалью и к искомой прямой (рис.2). Мы имеем нормаль и точку М0(1;-2), через которую проходит искомая прямая, поэтому используем уравнение прямой, проходящей через точку М(х 0, у 0) перпендикулярно вектору  . А(х-х 0)+В(у-у 0)=0, 2(х -1)+3(у +2)=0, 2 х +3 у +4=0.
. А(х-х 0)+В(у-у 0)=0, 2(х -1)+3(у +2)=0, 2 х +3 у +4=0.
б) Если искомая прямая l 1 (рис.3) перпендикулярна заданной l, то вектор  будет параллелен прямой l 1, и мы возьмем его в качестве направляющего вектора искомой прямой
будет параллелен прямой l 1, и мы возьмем его в качестве направляющего вектора искомой прямой  .
.
| l |
| l 1 |
| 2 х +3 у -3=0 |
 . .
|
| М(1;-2) |
| Рис.3 |
Используем уравнение прямой, проходящей через точку М(х 0, у 0) параллельно вектору 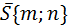 .
.  . У нас
. У нас  .
.  ; 3 х -3=2 у +4, 3 х -2 у -7=0.
; 3 х -3=2 у +4, 3 х -2 у -7=0.
Ответ: 2 х +3 у +4=0, 3 х -2 у -7=0.
2. Найти расстояние от точки М0(2;-1) до прямой 3 х +4 у -22=0.
Решение:
 ; х 0=2; у 0=-1.
; х 0=2; у 0=-1.
А=3; В=4; С=-22.
 .
.
Ответ: 4.






