Прямоугольная диметрическая проекция. Построение проекции.

Коэффициенты искажения в диметрической проекции выбирают следующими:

k = n; m = 1/2 k.

Тогда

2 k ²+ 1/4 k ²; m = 0,47

.

В целях упрощения построений, как и в изометрических проекциях, приведенный коэффициент искажения по осям x и z принимают равным 1; по оси у коэффициент искажения равен 0,5. По осям x и z или парал­лельно им все размеры откла­дывают в натуральную величину, по оси у размеры уменьшают вдвое.

Увеличение в этом случае составляет 6% (выражается числом 1,06 = 1:0,94). Расположение осей Ох и Oy в диметрическои проекции показано на рисунке 11.8. С достаточной для практических це­лей точностью оси x и у строят по тангенсам углов:

 

tg 7°10 ' 1/8; tg 42°25 ' 7/8.

 

Продолжение оси у за центр О_р является биссектрисой угла xО_р z, что также может быть использовано для построения оси у.

Окружности в диметрической проекции – на рисунке 11.10 с указанием соответствующих значений величин осей эллипсов для приведенных коэффициентов искажения, равных 1.

 

 

Рис.11.8

 

Большая ось эллипсов расположена под углом 90° для эл­липсов, лежащих:

в плоскости xOz – к оси у,

в плоскости yOz – к оси x,

в плоскости xOy – к оси z.

При выполнении аксонометрического изображения от руки (как рисунка) построение эллипсов, как в изометрии, так и в диметрии, выполняют по 8 точкам. Например, по точкам 1, 2, 3, 4, 5, 6, 7 и 8 (см. рис. 11.9). Точки 1, 2, 3 и 4 находят на соответствующих аксонометрических осях, а точки 5, 6, 7 и 8 строят по величинам соответствующих большой и малой осей эллипса.

При выполнении же аксонометрического изображения чер­тежным инструментом построение эллипсов в диметрической проекции также производят по 8 точкам, а эллипсы в изомет­рической проекции можно заменять овалами и строить их сле­дующим образом.

 

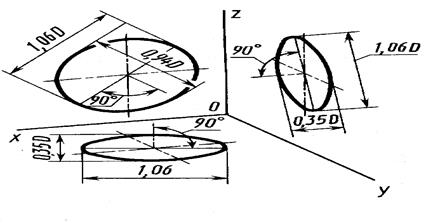Рис 11.10

 

Построение показано на рисунке 11.9 на примере эллипса, лежащего в плоскости xOz. Из точки 1 как из центра делают засечку радиусом R = D на продолжении ма­лой оси эллипса в точке О₁ (строят также аналогичным обра­зом и симметричную ей точку, которая на чертеже не показана). Из точки О₁ как из центра проводят дуту CSC ра­диуса D, которая является одной из дуг, составляющих кон­тур эллипса. Из точки О₂ как из центра проводят дугу радиуса О₂ S до пересечения с большой осью эллипса в точках О₃. Проводя через точки О_{1 ,} О₃ прямую, находят в пересечении с дугой CSC точку К, которая определяет О ₃ К – величину ра­диуса замыкающей дуги овала. Точки К являются также точ­ками сопряжения дуг, составляющих овал.

 

41.Косоугольная фронтальная диметрическая проекция. Из ко­соугольных аксонометрических проекций рассмотрим фронталь­ную диметрическую проекцию, широко используемую в учебном процессе. Положение аксонометрических осей для нее приведено на рисунке 11.13. Допускается применять фронталь­ные диметрические проекции с углом наклона оси у 30° и 60°. Коэффициент искажения по оси у равен 0,5, по осям x и z – 1. Окружности, лежащие в плоскостях, параллельных фрон­тальной плоскости проекций, проецируются на аксонометри­ческую плоскость проекций в окружность. Окружности, лежащие в плоскостях, параллельных горизонтальной и про­фильной плоскостям проекций, – в эллипсы (рис.11.14). Большая ось эллипсов 2 и 3 равна 1,07, малая ось – 0,33 диа­метра окружности. Пример косоугольной фронтальной диметрической проекции детали приведен на рисунке 11.15.

 

 

 

Рис. 11.13 Рис. 11.14 Рис. 11.15