Для наглядного изображения расположенных в пространстве относительно выбранных плоскостей проекций точек, линий, плоскостей, многогранников и т.д. используются проекции, называемые аксонометрическими (от древнегреческого «аксон» – ось, «метрио» – измеряю) или аксонометрией. Их часто используют для наглядного изображения конструкций приборов, машин на чертеже, особенно на начальных этапах конструирования.
Способ аксонометрического проецирования состоит в том, что данная фигура вместе с осями прямоугольных координат, к которым она отнесена в пространстве, проецируется параллельно на некоторую плоскость, принятую за плоскость аксонометрических проекций.
При параллельном проецировании, если направление проецирования перпендикулярно к аксонометрической плоскости проекций, аксонометрическую проекцию называют прямоугольной, если направление проецирования не перпендикулярно к плоскости проекций, аксонометрическую проекцию называют косоугольной. В прямоугольной аксонометрической проекции оси присоединенных прямоугольных координат располагают непараллельно плоскости аксонометрических проекций.
Применяемые в отечественной конструкторской документации аксонометрические проекции стандартизованы в ГОСТ 2.317-69.
Рассмотрим образование аксонометрической проекции на примере изображения параллелепипеда с квадратным основанием (рис.11.1) путем последовательного преобразования его ортогональных проекций вместе с осями.

Рис.11.1
При повороте параллелепипеда (рис.11.1, а) с осями x и у вокруг оси z по стрелке А на 45° получаем его изображение (рис. 11.1, 6) с повернутыми осями х1 и у1 и сохранившейся вертикальной осью z. При повороте изображения на профильной проекции с осями z", x", у" по стрелке Б на угол 30° получаем изображение (рис.11.1, в) с осями z"1, x"2, у"2, расположенными под некоторыми углами к аксонометрической плоскости Р (Рw). Параллельная проекция (рис.11.1, г) по стрелке В на плоскости P и является аксонометрической проекцией параллелепипеда с осями на плоскости Р. Аксонометрическую плоскость при этом не обозначают (ею является плоскость бумаги).
Проекции осей координат xp, yp, zp на плоскости аксонометрических проекций называют аксонометрическими осями (в дальнейшем индекс «р» будет опускаться).
При различном взаимном расположении осей координат в пространстве и плоскости аксонометрической проекции и при разных направлениях проецирования можно получить множество аксонометрических проекций, отличающихся друг от друга направлением аксонометрических осей и масштабами по ним. Это положение доказано теоремой К.. Польке, которая утверждает:
три отрезка произвольной длины, лежащие в одной плоскости и выходящие из одной точки под произвольными углами друг к другу, представляют параллельную проекцию трех равных отрезков, отложенных на прямоугольных осях координат от начала.
Рассмотрим направление аксонометрических осей и масштабы по ним для направления проецирования, перпендикулярного аксонометрической плоскости проекций, т. е. для прямоугольной аксонометрической проекции.


Рис.11.2 Рис.11.3
Аксонометрическое изображение сферы и способ вписывания сферических поверхностей. В прямоугольной аксонометрии поверхность сферы проецируется на аксонометрическую плоскость проекций в виде круга. Это позволяет использовать сферу для построения аксонометрических проекций тех фигур, в которые могут быть вписаны сферические поверхности. Так, например, аксонометрия поверхности вращения в этом случае может быть построена как огибающая сфер, вписанных в эту поверхность.
Коэффициент искажения. На рисунке 11.2 изображена пространственная система ортогональных координат Ox, Oy, Oz единичные отрезки e на осях координат и их проекции в направлении S на некоторую плоскость P, являющуюся аксонометрической плоскостью проекций. Проекции ex, ey, ez отрезка e на соответствующих аксонометрических осях Opxp, Opyp, Opzp в общем случае не равны отрезку e и не равны между собой. Отрезки ex, ey, еz являются единицами измерения по аксонометрическим осям – аксонометрическими единицами (аксонометрическими масштабами).
Отношения:



называют коэффициентами искажения по аксонометрическим осям.
В частном случае положение аксонометрической плоскости можно выбрать таким, что аксонометрические единицы – отрезки ех, ey, ez – будут все равны между собой или будет равна между собой пара этих отрезков.
При ех = eу = ez (k = m = n) аксонометрическую проекцию называют изометрической; искажения по всем осям в ней одинаковы. При равенстве аксонометрических единиц по двум осям, обычно при ех = ez ≠ ey (k = n ≠ m), имеем диметрическую проекцию. Если ех ≠ еу ≠ ez, то проекцию называют тpuметрической.
Аксонометрическая плоскость Р на рисунке 11.3 изображена так, что она пересекает все три координатные оси Ox, Oy, Oz в точках х, у, z соответственно. Рассмотрим прямоугольную аксонометрию. В этом случае отрезок ООр перпендикулярен плоскости Р. Отрезки Opx, Opy, Opz являются аксонометрическими проекциями отрезков Ох, Oy, Oz и представляют собой катеты прямоугольных треугольников, гипотенузы которых – отрезки Ox, Oy, Oz. Обозначим углы между осями координат и их проекциями на плоскости P через α, β, γ. Тогда:
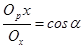

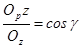
Эти отношения являются коэффициентами искажения, т. е.
k = cos α; m = cos β; n = cosγ.
Известно, что для отрезка OOр  Р сумма квадратов направляющих косинусов равна единице:
Р сумма квадратов направляющих косинусов равна единице:
cos 2 (π /2 – α) + cos 2 (π /2 – β) + cos 2 (π /2 – γ) = 1.
Отсюда:
sin 2 α + sin 2 β + sin 2 γ = 1
или
1 – cos 2 α + 1 – cos 2 β + 1 – cos 2 γ = 1.
Тогда:
cos 2 α + cos 2 β + cos 2 γ = 2
или
k 2 + m 2 + n 2 = 2,
т. е. сумма квадратов коэффициентов искажения равна 2.






