Пересечение двух плоскостей.

Прямая линия пересечения двух плоскостей определяется двумя точками, каждая из которых принадлежит обеим плос­костям, или одной точкой, принадлежащей двум плоскостям, и известным направлением линии. В обоих случаях задача за­ключается в нахождении точки, общей для двух плоскостей.

Общий прием построения линии пересечения двух плоскостей заключается в следующем. Вводят вспомогательную плоскость, строят линии пересечения вспомогательной плоскости с двумя за­данными и в пересечении построенных линий находят общую точку двух плоскостей. Для нахождения второй общей точки построение повторяют с помощью еще одной вспомогательной плоскости.

На рисунке 4.7 показано наглядное изображение линии пе­ресечения К₁К₂ двух плоскостей Р и Q.

Рис. 4.7 Рис. 4.8 Рис. 4.9

Для наглядного изображения построения первой общей точки линии пересечения плос-костей P и Q (рис.4.8) введена вспомогательная плоскость S. С плоскостью P она пересека-ется по линии 1– 2, с плоскостью Q – по линии 3 – 4. В пересечении линий 1 – 2 и 3 – 4 опре-делена первая общая точка К₁ двух плос­костей P и Q – первая точка линии их пересечения.

Аналогично вводят новую секущую плоскость и строят вто­рую точку линии пересечения.

Частный случай построения линии пересечения двух плоско­стей, когда одна из них проецирующая. Вэтом случае постро­ение линии пересечения упрощается тем, что одна ее проекция совпадает с проекцией проецирующей плоскости на ту плос­кость проекций, к которой она перпендикулярна.

В качестве примера на рисунке 4.9 показано построение проекций m'n', mn линии пересечения MN фронтально-про­ецирующей плоскости P с плоскостью треугольника ABC.

На фронтальной проекции в пересечении проекций a'b' и a'c' со следом P_v находим фронтальные проекции m' и n' двух общих точек заданных плоскостей. По ним построены гори­зонтальные проекции m и n на горизонтальных проекциях ab и ас сторон треугольника. Через точки m и n проводим горизон­тальную проекцию линии пересечения плоскостей. При взгляде по стрелке S по фронтальной проекции очевидно, что часть тре­угольника левее линии пересечения MN (m'n') находится над плоскостью P,т. е. видима, остальная часть – под плоскостью P,т. е. невидима (участок mbcn показан штриховой линией).

Другой пример построения линии пересечения двух тре­угольных пластин ABC и DEF, одна из которых (DEF)задана как горизонтально-проецирующая плоскость, приведен на рисунке 4.10.

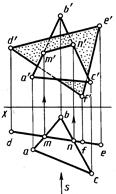
Рис. 4.10 Рис. 4.11

На горизонтальной проекции в пересечении гори­зонтальных проекций ab и bc сторон Δ ABC с проекцией dfe вто­рого треугольника находим горизонтальные проекции m и n точек их пересечения. По ним на фронтальных проекциях сторон a'b' и b'c' строим фронтальные проекции m' и n' точек линии пересечения MN. На фронтальной проекции отмечаем видимость ча­стей треугольников, руководствуясь следующим: при взгляде по стрелке S по горизонтальной проекции очевидно, что сторона А С находится перед плоскостью треугольника DEF.

Следовательно, сторона АС иограничиваемая ею часть тре­угольника ABC до линии пересечения MN видимы (т. е. види­ма фронтальная проекция четырехугольника a'c'n'm').Видимая часть фронтальной проекции Δ DEF на чертеже оттенена.

Построение линии пересечения плоскостей общего положения. На рисунке 4.11 приведено построение проекций m'n', mn линии пересечения двух плоскостей, одна из которых задана проекци­ями a'b', b'c', ab, bc двух пересекающихся прямых, другая – проекциями d'e', f'g', de, fg двух параллельных прямых.

В качестве вспомогательных плоскостей взяты две горизон­тальные плоскости, заданные следами R_v и T_v.

Плоскость R пересекает первую заданную плоскость по пря­мой 1 – 2,вторую – по прямой 3 – 4. По фронтальным проекци­ям 1 ', 2' и 3', 4' находим с помощью линий связи горизонтальные проекции 1, 2 и 3, 4 нагоризонтальных проекциях ab, bc, de, fg прямых. Через них проводим горизонтальные проекции линий 1–2 и 3–4 линиипересечения. Отмечаем точку m – гори­зонтальную проекцию общей точки M трех плоскостей – двух заданных и вспомогательной R. По ней определяем фронталь­ную проекцию m' на фронтальном следе R_v вспомогательной плоскости.

Вспомогательные плоскости T и R параллельны. Линии их пересечения с заданными плоскостями также параллельны. Поэтому горизонтальные проекции линий пересечения плос­кости T с заданными плоскостями проведены через проекцию b параллельно проекции

1–2 и через проекцию 5 параллельно проекции 3–4. В их пересечении найдена горизонтальная про­екция n второй общей точки трех плоскостей, т. е. линии пе­ресечения двух заданных плоскостей. По ней на фронтальном следе T_v вспомогательной плоскости построена фронтальная проекция n'. Через построенные проекции m', n' и m, n про­водим фронтальную и горизонтальную проекции искомой ли­нии пересечения MN.