Для построения кривой линии, получаемой при пересечении конической поверхности плоскостью, в общем случае находят точки пересечения прямолинейных или круговых образующих конической поверхности с секущей плоскостью. Соответствующий пример в случае пересечения фронтально-проецирующей плоскостью P (Pv) конуса с вершиной S приведен на рисунке 9.8.
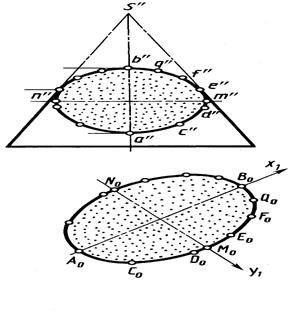Построение линии пересечения плоскости с конической поверхностью обычно выполняют в следующем порядке. Основание конуса делят на несколько равных частей (обычно 12), проводят горизонтальные проекции s – 1, s – 2,..., s – 12 образующих и строят их фронтальные проекции. На фронтальной проекции отмечают фронтальные проекции точек пересечения построенных образующих на видимой поверхности конуса с секущей плоскостью P (Pv): c', d', f', q', а также крайних точек а' и b'. Горизонтальные проекции строят в проекционной связи на соответствующих проекциях образующих – точки а, с, d, f, q, b на проекциях образующих s–1, s–2, s–3, s–5, s–6, s–7, a также симметричные им точки на проекциях образующих s–12, s–11, s–9, s–8. Горизонтальную проекцию e точки E на образующей S–4 и симметричной точки на образующей S–10 строят с помощью окружности радиуса е'е'1, проведенной на поверхности конуса.
На фронтальной проекции большая ось AB эллипса – линии пересечения фронтально-проецирующей плоскости с конусом – проецируется в натуральную величину: AB = a'b'. Малая ось MN эллипса перпендикулярна большой и проецируется в точку m'(n') в середине фронтальной проекции a'b' большой оси.
Построение горизонтальной проекции малой оси эллипса выполнено с помощью параллели с проекциями m'14' и m – 14 – n. Горизонтальная проекция mn малой оси эллипса построена в проекционной связи как хорда горизонтальной проекции m–14–n этой параллели. Профильная проекция линии среза конуса также построена по фронтальной и горизонтальной проекциям точек в проекционной связи.
Отметим, что на профильной проекции точки а" и а" низшая и высшая, m" и n"– край-ние (правая и левая), е" и симметричная ей – точки касания проекций крайних образующих.
Построение натурального вида фигуры среза A0M0B0N0 выполнено по координатам в системе координат х1 у1.
Наряду с построением эллипса по точкам возможно построение его по большой и малой осям.
При пересечении конической поверхности вращения плоскостью получаются различные линии – прямые, замкнутые кривые – окружности и эллипсы, незамкнутые кривые – параболы и гиперболы, а также точка. Вид указанных линий определяется положением секущей плоскости относительно вершины конической поверхности и соотношением между величинами углов наклона секущей плоскости и образующей конической поверхности к ее оси.
Рис. 9.6
Если секущая плоскость P (Рv) проходит через вершину (рис. 9.6, а), то пересечение плоскости с конической поверхностью в зависимости от угла а наклона плоскости к оси поверхности образует:
при β < α < (180° – β) – точку,
при α = β – прямую, по которой плоскость касается конической поверхности;
при 0 ≤α < β – две прямые (образующие).
Если плоскость пересекает коническую поверхность и при этом не проходит через вершину, то в их пересечении имеют место (рис. 9.6, б, в):
при α = 90° – окружность (плоскость, перпендикулярная оси, окружность AMB (a'm'b') в пересечении с плоскостью P (Pv) – рис. 9.6, б);
при β < α <(1800 – β) – эллипс (эллипс CMD (c'm'd') в пересечении с плоскостью Q (Qv) – рис. 9.6, б – плоскость пересекает все образующие конической поверхности);
при α < β – гипербола (плоскость параллельна двум образующим и пересекает коническую поверхность по обе стороны от вершины, например гипербола с вершинами E (e') и
F (f') в пересечении с плоскостью T (Tv) или с вершинами 1 (1') и 2 (2') в пересечении с плоскостью Т1 (Т 1v) – рис. 9.6, в);
при α = β – парабола (плоскость, параллельная одной из образующих, например парабола с вершиной К (k') в пересечении с плоскостью R (Rv) – рис. 9.6, в).
Наглядное изображение кривых – эллипса, гиперболы,
параболы, получающихся при пересечении конической поверхности плоскостями Q, T, R, приведено на рисунке 9.7.
