|
Нормальная плотность распределения (Гаусса)
Кривая нормальной плотности распределения описывается функцией 
,
которая называется гауссианой по имени германского математика К.Ф.Гаусса. Позднее были открыты многие замечательные свойства случайных величин, распределенных по нормальному закону. Ниже мы познакомимся с большинством этих свойств.Форма кривой нормальной плотности представлена на рис. 17. Это симметричная одномодальная плотность распределения, поэтому математическое ожидание, мода и медиана совпадают: 
.Дисперсия, четвертый центральный момент, асимметрия и эксцесс равны: 
, 
, As = 0,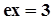 
.
В некоторых источниках эксцесс плотности распределения определяют по отношению к эксцессу нормальной плотности распределения. Тогда эксцесслюбого распределения уменьшается на 3, а эксцесс нормального распределения равен 0: 
.Принадлежность случайной величины к нормальной генеральной совокупности с математическим ожиданием c и дисперсией 
мы будем обозначать следующим образом 
.Характеристическую функцию нормальной случайной величины приведем здесь без вывода: 
.
Обратим внимание на то, что приотсутствия сдвига плотности распределения относительно начала координат, то есть при c = 0 множитель 
пропадает.
Интегральная функция нормального распределения выражается интегралом от плотности распределения: 
.Этот интеграл не может быть записан в конечной форме, поэтому его значения табулируются. В связи с тем, что этот интеграл зависит от параметров с и , которые могут принимать бесчисленное множество значений, в целях удобства табулирования эти параметры исключаются путем замены переменной интегрирования: 
.Тогда, пользуясь тем, что нормальная плотность распределения симметрична и F(c)=0.5, получим для 
:
где функция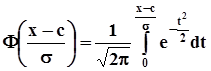 
называется функцией Лапласа. Таблицы этой функции приводятся во всех без исключения справочниках, учебниках и учебных пособиях по теории вероятностей и математической статистике. Если 
, 
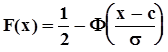. Оба эти выражения распространяются на всю ось путем объединения с использованием знаковой функции sign[·]: 
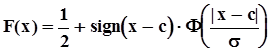.Вероятностная мера полуоткрытого интервала (a, b] вычисляется, как 
.Если интервал симметричен относительно математического ожидания, то есть границы интервала суть (c - a, c + a], то 
.На практике часто используются интервалы, ширина которых исчисляется целыми значениями среднеквадратического отклонения s. Наиболее популярными среди них являются: a = s, a = 2s, a = 3s. Для этих значений 
. Соответственно, вероятностные меры интервалов: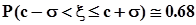 
, 
, 
.
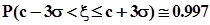14.Принцип вычисления вероятностной меры интервала при нормальном распределении случайной величины. 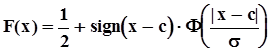-интегральная ф-цинормального распределения,где 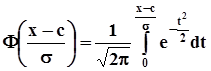-ф-ция ЛапласаВероятностная мера полуоткрытого интервала (a, b] вычисляется, как .
Если интервал симметричен относительно математического ожидания, то есть границы интервала суть (c - a, c + a], то .На практике часто используются интервалы, ширина которых исчисляется целыми значениями среднеквадратического отклонения s. Наиболее популярными среди них являются: a = s, a = 2s, a = 3s. Для этих значений . Соответственно, вероятностные меры интервалов: , , .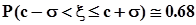
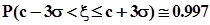15.Интегральная теорема Муавра-Лапласа и центральная предельная теорема(без док-ва),безграничная делимость нормальной плотности распределения два из многих исключительных свойств нормального распределения вероятностей: интегральная теорема Муавра-Лапласа и Центральная Предельная Теорема ( ЦПТ ).
Интегральная теорема Муавра-Лапласа основывается на локальной теореме Муавра-Лапласа. Напомним, что если в схеме Бернулли (см. п. 1.2.4) количество испытаний возрастает, т.е. n ®¥, а вероятность p появления одного из двух противоположных событий не изменяется, то в соответствии с локальной теоремой Муавра-Лапласа 
Интегральная теорема Муавра - Лапласа посвящена задаче упрощенной оценке вероятности 
без необходимости трудоемких вычислений числа сочетаний. На основании локальной теоремы 
.Последнее равенство является точным в условиях действия локальной теоремы Муавра-Лапласа в связи с тем, что из-за дискретности случайной величины 
m = 1. В то же время последняя сумма есть не что иное, как формула прямоугольников приближенного вычисления интеграла: 
.В конечном итоге при n ®¥ и при p = const интегральная теорема Муавра - Лапласа утверждает следующую ассимптотику 
. Центральная Предельная Теорема (ЦПТ). Приведем упрощенную формулировку теоремы. Плотность распределения суммы независимых произвольно распределенных случайных величин, дисперсии которых различаются не слишком сильно, при увеличении числа слагаемых стремится к нормальной плотности распределения.
Распределение вероятностей случайной величины безгранично делимо тогда и только тогда, когда эта случайная величина может быть представлена суммой любого количества независимых случайных величин, подчиненных тому же распределению вероятностей
