|
Плотность распределения Arcsin График плотности распределения приведен на рис. 15. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией 
.Математическое ожидание и медиана совпадают: 
.Дисперсия, четвертый центральный момент, асимметрия и эксцесс равны: 
, 
, As = 0, 
.Случайная величина с такой плотностью распределения возникает при аналого-цифровом преобразовании, например, синусоидального напряжения, действующего на входе аналого-цифрового преобразователя 
(АЦП). При запуске АЦП в случайные моменты времени или в моменты времени, не синхронизированные с частотой напряжения помехи, как видно из рис. 16, из-за плоских максимумов и минимумов синусоиды плотность значений выходного сигнала АЦП возрастает к краям интервала 
и минимальна в середине этого интервала. Интегральная функция распределения описывается функцией, обратной функции y = sin x, то есть функцией
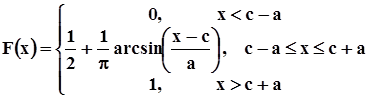
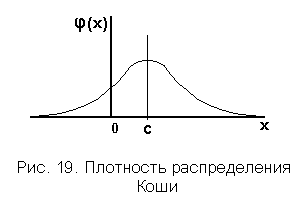
Плотность распределения Коши График плотности распределения приведен на рис. 19. Плотность распределения симметрична относительно математического ожидания. Кривая плотности распределения описывается функцией 
Плотность распределения симметрична, одномодальна. Изобщего выражения для моментов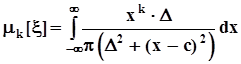 
|
видно, что при всех целых значениях k> 0 этот несобственный интеграл не существует, поскольку порядок убывания подинтегральной функции на бесконечности при k> 0 не превышает единицы. При k = 0 этот интеграл равен 1, что и должно следовать из условия нормировки плотности распределения.
В связи с этим математическое ожидание, дисперсия и моменты более высоких порядков случайной величины, распределенной по Коши, отсутствуют. Параметры плотности распределения Коши имеют названия: c - параметр сдвига ( совпадает с модой и медианой ), D - параметр масштаба. Эксцесс случайной величины, распределенной по Коши, равен ¥. Характеристическая функция
.
Справедливость этого выражения обнаруживается при сопоставлении пары преобразований Фурье, связывающих плотность распределения Лапласа с ее характеристической функцией при c = 0. Здесь вид характеристической функции с точностью до множителя совпадает с видом плотности распределения Лапласа, а вид характеристической функции плотности Лапласа с точностью до того же множителя совпадает с видом плотности распределения Коши. Заметим, что характеристическая функция случайной величины, распределенной по Коши, недифференцируема в нуле, и это - еще один признак отсутствия моментов данной случайной величины.
