Характеристическая функция непрерывной случайной величины

 

Характеристической функцией непрерывной случайной величины x называется математическое ожидание случайной функции 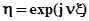: 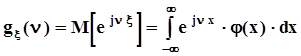. Иными словами, характеристическая функция случайной величины есть интегральное преобразование плотности распределения этой случайной величины. Это преобразование есть частный случай применения обратного преобразования Фурье к функциям, обладающим специфическими свойствами, присущими плотности распределения, а именно, к неотрицательным функциям, интеграл от которых по всему множеству их определения равен 1. Отсюда следует, что характеристическая функция и плотность распределения связаны взаимно однозначно, то есть . Приведем здесь несколько полезных свойств характеристической функции, первое из которых порождено спецификой плотности распределения случайной величины.

a) При n = 0

,

,.................................

.

Приведенные равенства означают, что для определения начальных моментов всех порядков достаточно знать выражение для характеристической функции, продифференцировать его k раз по аргументу n, подставить в полученную производную значение n = 0 и разделить результат на . В частности, если необходимо определить дисперсию, то придется найти первый и второй начальные моменты и затем воспользоваться соотношением, которое было получено ранее в п. 1.3.3: .

b) Если задана случайная величина h, которая является линейной функцией случайной величины x: h = a×x + b, то характеристическая функция случайной величины h есть . Это свойство, в частности, означает, что при простом смещении значений случайной величины по оси абсцисс на величину b характеристическая функция умножается на экспоненту в степени jnb. То есть, если h = x + b, то .

с) Пусть имеется последовательность плотностей распределения непрерывных случайных величин. Пусть 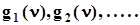- характеристические функции этих случайных величин. Если последовательность плотностей распределения сходится и предельная плотность распределения есть j(x), то последовательность характеристических функций также сходится и имеет предельную функцию g(n), которая есть характеристическая функция случайной величины с предельной плотностью распределения j(x). Иными словами, из сходимости плотностей распределения случайных величин следует сходимость их характеристических функций. Справедливо и обратное утверждение: из сходимости характеристических функций случайных величин следует сходимость их плотностей распределений. Это свойство очевидным образом следует из взаимно однозначной связи между характеристическими функциями и плотностями распределения.Необходимые условия того, чтобы некоторая функция g(n) была характеристической функцией:a) g(n) непрерывна по n, b) g(n) определена на каждом конечном интервале n, c) g(0) = 1, d) |g(n)| £ 1.

Примеры

Найдем характер ф-цию для плотности распределения Лапласа:

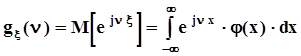- ф-ла характ ф-ции

1) - плотность распредел. Лапласа.

2) - плотность распр Коши - параметр масштаба. с-параметр сдвига(совпадает с модой и медианой),тогда

3) - плотность распред Пуассона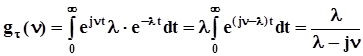

10.Поток Пуассона,плотность распределения вероятностей интервалов времени между событиями в потоке Пуассона,вывод,характеристическаяфункция,моменты,график плотности распределения. Случайная величина - интервал времени между импульсами в простейшем случайном потоке Простейшийслучайный поток импульсов, заявок на обслуживание и тому подобных последовательностей случайных событий задается следующими свойствами:- поток импульсов (заявок) рассматривается в течение интервала времени, равного t, - в любом бесконечно малом, но не нулевом промежутке времени Dt, на которые поделен интервал времени (0, t] и который будем называть элементарным промежутком, с вероятностью p> 0 может появиться только один импульс (одна заявка),

- появление импульса (заявки) в каждом из элементарных промежутков времени Dt есть событие, не зависящее от предистории, то есть от появления импульса (заявки) в преды­дущие промежутки времени, это свойство именуется, как отсутствие последействия или как отсутствие памяти.

Такие условия осуществления событий, которые заключаются в случайном появлении импульсов (заявок) в следующие друг за другом элементарные промежутки времени, в точности соответствуют схеме Бернулли последовательности независимых испытаний. Если n - количество элементарных промежутков на интервале (0, t], то t = n×Dt, а np - математическое ожидание количества импульсов (заявок) на этом интервале (то есть среднее значение их количества).Тогда естественным образом может быть вычислена средняя частота или интенсивность следования импульсов (заявок) в течение интервала (0, t], как отношение среднего их количества за этот интервал к длительности интервала, то есть 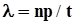. Отсюда, в частности, следует, что np = lt. Единица измерения частоты l есть [1/c]. Найдем функцию распределения непрерывной случайной величины t -времени между двумя последовательными импульсами (заявками) в потоке:

. Неравенство выполняется в случаях, когда за время t появляется один импульс (заявка), или 2 импульса (заявки), или 3 импульса (заявки) и так далее. Определить вероятность бесконечного объединения подобных событий затруднительно. Гораздо легче и продуктивнее определить эту вероятность через вероятность противоположного события, а именно, через вероятность того, что за время t не появится ни одной заявки (отказа, импульса), то есть . Напомним, что исходной моделью для модели простейшего потока была схема независимых испытаний Бернулли. Поскольку потоки указанных событий реализуются в непрерывном времени, устремим Dt к нулю, при этом n ®¥, 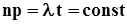, и с использованием теоремы Пуассона найдем вероятность появления m импульсов в n интервалах времени, или, что то же самое, в течение времени t, как предел: 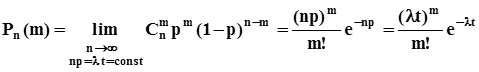. Вероятность того, что в течение времени t не появится ни одного импульса (или ни одной заявки), то есть m = 0, равна . Отсюда функция распределения интервала времени между двумя последовательными импульсами (заявками) в случайном потоке равна . Плотность распределения этой случайной величины есть производная от F(t) по t: . В результате мы получили экспоненциальную плотность распределения или экспоненциальный закон распределения. Вид кривой экспоненциальной плотности распределения при различных значениях параметра l представлен на рис. 13. Фигуры, ограниченные кривой плотности распределения и осями абсцисс, равновелики, их площади равны 1. Характеристическая функция экспоненциального распределения вычисляется, по определению, как интеграл

.

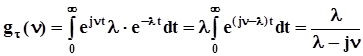Математическое ожидание и дисперсию случайного интервала времени между событиями (заявками, отказами, импульсами) находим, пользуясь свойствами характеристических функций:

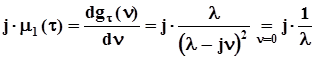,откуда .

,откуда 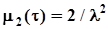и . Стало быть, среднеквадратическое значение . При статистической обработке экспериментальных данных, когда возникает необходимость идентификации вида плотности распределения исследуемой случайной величины, последнее соотношение может служить одним из признаков экспоненциального распределения.Сформированная таким образом математическая модель случайной последовательности событий называется простейшим потоком или потоком Пуассона и применяется в теории массового обслуживания и в теории надежности для вероятностного описания таких потоков, как например,- потока вызовов на телефонную станцию, - потока обращений к серверу коллективного пользования в компьютерной сети,- потока автомобилей на пограничный пункт таможенного досмотра,- потока клиентов на обслуживающее предприятие, - потока отказов технического устройства и т.д. Наряду с простейшим потоком в теории массового обслуживания используются и более сложные модели потоков заявок, такие, как, например, потоки Эрланга и Пальма, однако, наиболее полные аналитические описания всех процедур и характеристик обслуживания заявок, потоков необслуженных заявок, длины очередей на обслуживание и тому подобных характеристик существуют пока только для простейших потоков.В теории надежности F(t) называется функцией распределения времени безотказной работы устройства, а вероятность P(t) = 1 - F(t) = - функцией надежности. Математические модели случайных потоков событий применяются для анализа и синтеза систем, в которых подобные потоки возникают. Целью анализа и расчета таких систем может быть, например, оценка вероятности того, что обслуживание заявки не состоится, и заявка пропадает - оценка средней длины очереди заявок на обслуживание,- анализ и синтез стратегии обслуживания заявок,- расчет времени безотказной работы сложных систем

Случайные величины с плотностями распределения вероятностей:равномерной и Лапласа;графики,характеристическая функция последней,числовые характеристики,моменты,примеры по заданию экзаменатора.