|
Вначале введем и кратко опишем гамма - функцию, которая встретилась уже и будет встречаться в дальнейшем.Введем математическое определение гамма - функции и применим интегрирование по частям: 
,где 
, 
, 
, 
.Выполним подстановку: 
= 
.В результате мы получили рекуррентную формулу для вычисления значений гамма - функции.Если x - целое положительное число, x = n, то в соответствии с этой рекуррентной формулой имеем 
.Вычислим G(1) отдельно: 
Поэтому 
В частности, G(1) = 0×Г(0) = 0! = 1. В дальнейшем нам понадобятся следующие значения гамма - функции от дробных аргументов: 
, 
, 
.Последние два значения гамма-функции получены с использованием только что выведенной рекуррентной формулы.Пусть задана непрерывная дифференцируемая функция от случайной величины x: h = f (x). Известна плотность распределения случайной величины x: j (x). Задача состоит в том, чтобы найти плотность распределения y(y) случайной величины h. Подобная задача возникает в технике, когда случайные процессы или измеряемые величины, возмущенные случайными помехами, претерпевают нелинейные преобразования, и возникает задача прогнозирования характеристик сигнала, который получается в результате этого преобразования.Для вывода необходимого соотношения воспользуемся рис. 20. На этом рисунке представлены: функция преобразования y = f(x) и плотность распределения j(x). Функция преобразования предполагается монотонной, и это свойство функции преобразования практически всегда имеет место в технических устройствах: средствах измерения, измерительныхпреобразователях и регуляторах. В силу взаимной однозначности преобразования случайная величина h принимает значения из интервала Dy, в точности с той же вероятностью, с которой случайная величина x принимает значения из интервала Dx. Поскольку вероятностная мера интервала есть площадь под кривой плотности распределения на этом интервале, это означает, что площади заштрихованных фигур на рис. 20 должны быть равны: 
,где 
, 
- точки, находящиеся внутри выделенных интервалов Dx и 
, 
- значение искомой плотности распределения в точке .Из этого выражения следует: 
.Заметим здесь, что ширина интервала , в который преобразуется интервал Dx, не зависит от знака производной функции преобразования, и это обстоятельство мы учтем при выполнении предельного перехода 
.В силу инвариантности первого дифференциала производная 
выражается через производную от обратной функции: 
Кроме того в выражении для y(y) необходимо выразить аргумент x плотности распределения j(x) через y с помощью обратной функции: 
. В итоге окончательно получим: 
. Пример: Случайная величина h образуется в результате линейного преобразования случайной величины 
: 
. В данном случае реализуется функциональное преобразование 
, обратная функция 
, производная от нее по y равна 
. В результате подстановки в общую формулу получим: 
.Это означает, что любое линейное преобразование не изменяет вид плотности распределения случайной величины. Изменяется лишь масштаб и смещение от начала координат.
|
17.Вывод формулы для плотности распределения случайной величины 
и для ее характеристической функции,гдеx–случайная величина с нормальной плотностью распределения N(0;1) Случайная величина x распределена нормально: 
. Функция преобразования . Эта ситуация представлена на рис. 21. Из рисунка видно, что в силу двузначности обратной функции случайная величина h принимает значения из интервала , когда случайная величина x принимает значения в одном из двух выделенных интервалов Dx. Поэтому для данного примера исходное выражение должно быть изменено следующим образом: 
. Из этого следует соответствующее изменение общей формулы: 
. Для данного примера 
, 
, 
,
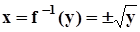В конечном итоге, после подстановки в общую формулу получим искомую плотность распределения: 
.Найдем характеристическую функцию этого распределения.
.Сделаем замену переменной интегрирования:
.В результате этой замены получим выражение с участием гамма-функции:
Поскольку 
, окончательно получим: 
18.Вывод формулы для плотности распределения 
,где 
–произвольная функция распределения непрерывной случайной величины Пусть - интегральная функция распределения случайной величины x. Образуем случайную величину h, как функцию от случайной величины x: . Задача состоит в том, чтобы найти плотность распределения y (y) случайной величины h. Воспользуемся полученным ранее выражением 
.В нашем случае в качестве функции y = f(x) выступает функция 
, производная от которой по x есть плотность распределения j(x). Поэтому 
.Таким образом, оказывается, что случайная величина h, полученная в результате функционального преобразования любой непрерывной случайной величины x путем ее подстановки в ее же интегральную функцию распределения, распределена равномерно в интервале [0,1] вне зависимости от вида функции распределения величины x. Полученный результат имеет два полезных применения. Первое. Машинное моделирование случайных чисел с заданной интегральной функцией распределения. Технология моделирования такова:- задается функция распределения F(x),- по стандартным программам генерируются случайные числа 
, распределенные равномерно в интервале [0, 1], - случайные числа 
, распределенные в соответствии с заданной функцией распределения F(x) получаются, как решения уравнений 
. Второе. Статистическое оценивание параметров и характеристик случайных величин по результатам экспериментов, вне зависимости от вида распределения исследуемой случайной величины. Это применение будет изложено ниже в разделе 2. Математическая статистика.
