Общий вид линейного преобразования случайного вектора есть умножение его на матрицу и добавление произвольного неслучайного вектора: 
.Раскроем это преобразование: 
.Вычислим вначале математическое ожидание от первой составляющей первого извекторов: 
. Точно так же 
. Поэтому 
.
В соответствии с математическим определением ковариационной матрицы 
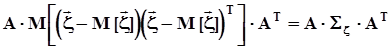Таким образом, если случайный вектор 
претерпевает преобразование , то математическое ожидание и ковариационная матрица результата такого преобразования вычисляются по формулам: 
, 
.Мы снова убеждаемся в том, что ковариационная матрица не зависит от смещения, которое задается вектором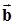 
.Рассмотрим в качестве примера один важный частный случай.Пусть матрица A имеет вид 
, а вектор 
. Тогда y - скаляр: y = 
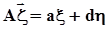, и ковариационная матрица 
также вырождается в скаляр, а именно - в дисперсию, которую будем обозначать через 
Найдем математическое ожидание и дисперсию случайной величины y, пользуясь полученными формулами.
. Перемножив эти два вектора, окончательно получим 
Частные случаи:- случайные величины x и h независимы или хотя бы некоррелированы, тогда 
, - коэффициенты a = b = 1, то есть случайная величина y есть сумма двух некоррелированных случайных величин x и h, тогда 
, то есть дисперсия суммы некоррелированных случайных величин равна сумме дисперсий слагаемых Пусть в одинаковых условиях выполнены две серии независимых испытаний по схеме Бернулли (см. п. 1.2.4). Количество испытаний в первой серии равно n, во второй серии - k. Производящие функции моментов: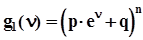 
и 
. Найти производящую функцию моментов для случайной величины - суммы количества появления события A в этих двух сериях испытаний. Искомая функция есть произведение: 
.Оказывается, что полученная функция - это производящая функция моментов биномиального распределения, соответствующего схеме Бернулли с количеством испытаний, равным (n+k). Конец примера. Полученный результат свидетельствует о том, что сумма случайных величин, подчиняющихся биномиальному распределению, есть случайная величина, распределенная также по биномиальному закону. Это свойство случайных величин и их распределений называется безграничной делимостью. Приведем точную формулировку обнаруженного свойства. Распределение вероятностей случайной величины безгранично делимо тогда и только тогда, когда эта случайная величина может быть представлена суммой любого количества независимых случайных величин, подчиненных тому же распределению вероятностей
Непрерывные случайные величины, аксиоматика,функции распределения и плотности распределения вероятностей,свойства,числовыехарактеритики,квантили,интерквантильныйпромежуток,неравенство Чебышева.
