Рассмотрим приближенный метод решения нелинейных уравнений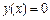 
на примере уравнения 
.
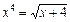Для данного уравнения уже выполнено отделение корней. Пусть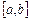 
один из отрезков, содержащих только один корень.
Формула метода итераций имеет вид:
Знак перед дробью, для нахождения коэффициента 
берется обратным к знаку производной.
За начальное приближение можно взять середину отрезка, т.е. 
Вычисления завершаются тогда, когда для найденного значения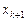 
выполняется условие 
, значение корня при этом будет равно .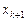
Пример: Найти корень уравнения 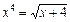методом итераций с точностью 
Выбираем один из найденных отрезков, содержащих только один корень (рис. 13). Для выбранного отрезка находим точку начального приближения
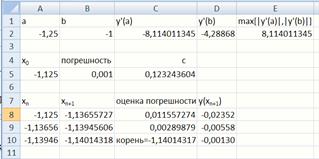
Рис. 13. Вид экрана для метода простых итераций
В ячейку А2, В2 (рис. 13) записываем исходные данные. В ячейки С2, D2 ввести формулы вычисления производных данной функции. Формула для заполнения ячейки E2 (рис.14). Формула для заполнения ячейки C5 (рис.15). Формула для заполнения ячейки B8 (рис.16). В ячейку А9 устанавливаем ссылку на В8.
Рис. 14. Формула для заполнения ячейки E2
Рис. 15. Формула для заполнения ячейки C5
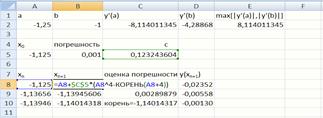
Рис. 16. Формула для заполнения ячейки B8
Задания для самостоятельного выполнения.
Из таблицы 2 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Найти корни уравнения методом простых итераций для всех отрезков, содержащих единственный корень.
Контрольные вопросы
1. Метод простых итераций решения нелинейных уравнений.
2. Сравните метод простых итераций с другими методами.
Численные методы решения системлинейных уравнений
Решение систем линейных уравнений методом простых итераций методом зейделя
Метод простых итераций. Рассмотрим метод простых итераций на примере системы литейных уравнений размерности 
Для сходимости этого метода достаточно выполнения условия доминирования диагональных элементов системы. Для системы размерности 
данные условия имеют вид:
Формулы для вычисления 
шага метода простых итераций:
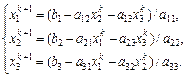
В качестве нулевого приближения используются значения 
или 
Итерационный процесс продолжается пока не будет выполнено условие:
Пример 1: Решить систему линейных уравнений
методом простых итераций с точностью
Ввести исходные матрицы А и В (рис. 17), также точность вычисления Заполнить заголовок таблицы.
В ячейки A7:C7 ввести нулевое приближение. В качестве нулевого приближения используются значения или В ячейки A8:C8 ввести формулы метода простых итераций (рис.18).
Рис. 17. Вид экрана для метода простых итераций
Рис. 18. Формула для заполнения ячейки А8
Заполнить блок вычисления 
(рис.19), далее заполняем ячейки G8, H8 (рис. 20-21).
Рис. 19. Формула для заполнения ячейки D8
Рис. 20. Формула для заполнения ячейки G8
Рис. 21. Формула для заполнения ячейки H8
Протянуть восьмую строку до тех пор, пока в ячейке H8 не появится надпись “стоп”.
Метод Зейделя. В отличии от метода простых итераций в методе Зейделя есть изменения во второй и третьей итерационных формулах:
Данное изменение позволяет ускорить сходимость итерационного процесса.
Пример 2: Решить систему линейных уравнений
методом Зейделя с точностью
Скопировать метод простых итераций и в ячейки В17, С17 внести изменения в соответствии с формулами метода Зейделя (рис. 22).
Рис. 22. Вид экрана для метода Зейделя
Рис. 23. Проверка методом обратной матрицы
Выполнить проверку решения системы линейных уравнений методом обратной матрицы (рис. 23).
Задания для самостоятельного выполнения.
Из таблицы 3 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Предварительно проверить выполнение условия доминирования диагональных элементов. Если данное условие не выполняется, преобразовать систему линейных уравнений с помощью элементарных эквивалентных преобразований. Найти решение системы линейных уравнений методом простых итераций и методом Зейделя. Выполнить проверку решения методом обратной матрицы.
Контрольные вопросы
1. Метод простых итераций решения систем линейных уравнений.
2. Метод Зейделя решения систем линейных уравнений.
3. Достаточное условие для применений указанных методов.
