Способы отделения корней уравнений
Рассмотрим приближенные методы решения нелинейных уравнений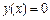 
на примере уравнения 
.
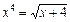При использовании некоторых методов в качестве исходных данных необходимо указать отрезок, содержащий только один корень данного уравнения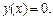 
Поиск такого отрезка называется отделением корней уравнения. Отделение корней можно проводить двумя способами: графическим и аналитическим.
Графический метод. Действительным корням уравнения 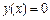соответствуют точки пересечения графика функции 
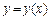с осью Ох. Для нахождения отрезка, содержащего только один корень уравнения, достаточно построить график функции 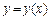и визуально определить на каких отрезках находятся корни. Точность отделения отрезков зависит от точности построения графиков.
Пример 1: Выполнить отделение корней уравнения 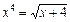графическим методом.
Для решения данной задачи требуется построить график функции 
Протабулируем данную функцию. Сначала определимся с областью построения, например, выберем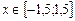 
, с шагом 0,25 будем вычислять значение функции (см. рис. 2)
Далее с помощью мастера диаграмм, выбрав тип диаграммы точечная, постоим график функции, представленной таблично. (см. рис. 3)
На рисунке 3 видно, что точки пересечения графика функции 
с осью Ох попадают в отрезки 
и 
.
Аналитический метод. В основе данного метода лежат теоремы математического анализа.
Рис. 2. Таблица функции
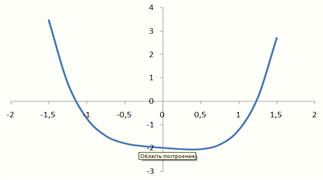
Рис. 3. График функции
Теорема 1 (Теорема Больцано-Коши). Если непрерывная на отрезке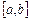 
функция 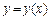на концах указанного отрезка принимает значения разных знаков, т.е. 
то на интервале 
она хотя бы один раз обращается в нуль.
Теорема 2. Непрерывная монотонно возрастающая или монотонно убывающая функция 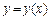имеет единственный нуль на отрезке 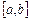тогда и только тогда, когда на концах указанного отрезка она принимает значения разных знаков, т.е. 
Пример 2: Выполнить отделение корней уравнения 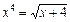аналитическим методом.
Для решения данной задачи требуется протабулировать функцию на некотором отрезке, например, 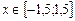и определить «соседние» точки, в которых функция принимает значения разных знаков.
Шаг табулирования выбираем произвольно, т.о. заполняем ячейки А1:С2 (рис. 4). Далее в ячейку А5 записываем ссылку на ячейку А1, в ячейку А6 записываем формулу, см. рисунок 5. С помощью маркера автозаполнения в первом столбце производим дальнейшие вычисления.
Заполняем столбец B5:B17, для этого в ячейку B5 записываем формулу вычисления функции и протягиваем ее вниз.
Рис. 4. Вид экрана для аналитического метода отделения корней
Рис. 5. Формула для заполнения ячейки А6
В ячейку С6 вводится комментарий (ячейка С5 остается пустой), он поможет определить отрезки, на концах которых функция принимает значения разных знаков (рис. 6).
В столбцах D и E записываются формулы для вычисления первой и второй производных данной функции.
Рис. 6. Формула для заполнения ячейки С6
В итоге видим, что найдены два отрезка, содержащие только один корень. Убедитесь в справедливости теоремы 2 для данных отрезков самостоятельно.
Задания для самостоятельного выполнения.
Из таблицы 2 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Выполнить отделение корней для функции своего варианта двумя способами графическим методом и аналитически. Начальные данные и шаг подобрать в зависимости от вида уравнения и области его определения.
Контрольные вопросы
1. Как записать основные математические функции в Excel.
2. Сформулируйте алгоритм графического метода отделения корней.
3. Сформулируйте теорему 1 и теорему 2. В чем их отличия и сходства.
4. Сформулируйте алгоритм аналитического метода отделения корней.
