Рассмотрим приближенные методы решения нелинейных уравнений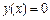 
на примере уравнения 
.
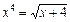Для данного уравнения уже выполнено отделение корней. Пусть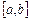 
один из отрезков, содержащих только один корень. Тогда любуюточку отрезка можно принять за приближенное значение корня, при этом 
Если задана допустимая погрешность 
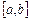, то задача сводится к задаче отыскания отрезка , содержащего только один корень уравнения и при этом 
Метод бисекций. Отрезок 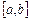делится пополам точкой 
и далее рассматриваются два отрезка: 
и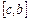 
. Затем выбирается один из них, для которого выполняется условие теоремы 2, выбранный отрезок переобозначается 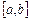и снова делится пополам. Получаем систему вложенных отрезков.
Корень считается найденным, когда для последнего отрезка будет выполняться условие За приближенное значение принимается его середина.
Пример 1: Найти корень уравнения 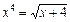методом бисекций с точностью 
Выбираем один из найденных отрезков, содержащих только один корень.
В ячейки А5, В5 (рис. 7) записываем относительные ссылки на исходные концевые точки отрезка. В ячейку С5 записываем формулу со ссылками на ячейки А5, В5, далее вычисляются значения функции 
,в качестве аргументов используются ссылки А5, В5, С5.
Рис. 7. Вид экрана для метода бисекций
В ячейку G5 записывается формула оценки погрешности(рис. 8).
Рис. 8. Формула для заполнения ячейки G5
В ячейке А6 выбирается одно из значений 
или 
, для которого выполняется условие теоремы 2 (рис. 9). Аналогичная формула записывается в ячейке В6.
Все остальные ячейки заполняются с помощью маркера автозаполнения до тех пор, пока не появится надпись «корень=»в столбце G.
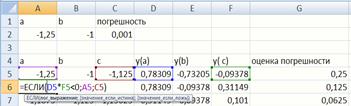
Рис. 9. Формула для заполнения ячейки А6
Метод хорд. Отрезок 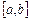делится точкой 
и далее рассматриваются два отрезка: и 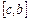. Затем выбирается один из них, для которого выполняется условие теоремы 2, выбранный отрезок переобозначается 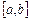и снова делится. Получаем систему вложенных отрезков.
Корень считается найденным, когда для отрезка будет выполняться условие 
За приближенное значение принимается 
.
Пример 2: Найти корень уравнения 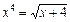методом хорд с точностью
Используем шаблон для вычисления корня методом бисекций (рис. 10). Вносим изменения в ячейку С5, записываем формулу (точка пересечения хорды с осью Ох) и протягиваем ее вниз. В ячейку G6 записываем формулу оценки погрешности и поиска корня, а ячейку G5 оставляем пустой. С помощью маркера автозаполнения находим ответ.
Рис. 10. Вид экрана для метода хорд
Задания для самостоятельного выполнения.
Из таблицы 2 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Найти корни уравнения методом бисекцийи методом хорд для всех отрезков, содержащих единственный корень.
Контрольные вопросы
1. Метод бисекций решения нелинейных уравнений.
2. Графическая реализация метода бисекций.
3. Метод хорд решения нелинейных уравнений.
4. Графическая реализация метода хорд.
