Приближенное решение обыкновенных дифференциальных уравнений
Требуется найти на отрезке 
решение обыкновенного дифференциального уравнения 
при заданном начальном условии 
Решением дифференциального уравнения называется такая дифференцируемая функция, которая при подстановке в уравнение обращает его в верное равенство. Рассмотрим численные методы решения данной задачи.
Разобьем отрезок на 
равных частей точками 
Метод Эйлера. Решение обыкновенного дифференциального уравнения при заданном начальном условии можно определить по итерационной формуле Эйлера:
Геометрический смысл метода Эйлера заключается в аппроксимации решения отрезком касательной приведенной к графику в левой точке отрезка. Затем строится касательная к кривой в правой точке отрезка и переносится параллельно до совмещения с концом касательной, построенной на предыдущей итерации и т.д. Полученная ломаная и есть приближенное решение.
На практике при решении дифференциального уравнения численными методами часто требуется обеспечить точность вычисления 
Для оценки точности выполняют два расчета с числом разбиений и 
Вычисления заканчиваются, если 
при невыполнении неравенства число разбиений удваивается и вновь производится сравнение результатов.
Пример 1: Найти решение дифференциального уравнения 
на отрезке 
при начальном условии 
используя метод Эйлера. Обеспечить точность вычисления 
Рис. 36. Численное решение дифференциального уравнения методом Эйлера
Вводим отрезок , начальное условие (С2), 
(D2), 
(E2)(рис. 36).
Вычисляем блок А5:А15 самостоятельно. Для заполнения ячейки В5 используется формула =C2. Для заполнения ячейки В6 используется формула =B5+$E$2*(2*A5^3-B5^2), далее она протягивается вниз и заполняем весь столбец В.
Выполняем решение дифференциального уравнения методом Эйлера при 
Исправленный метод Эйлера. Решение обыкновенного дифференциального уравнения при заданном начальном условии можно определить по итерационной формуле исправленного метода Эйлера:
Геометрический смысл исправленного метода Эйлера заключается в следующем. Строится касательная к графику в левой точке отрезка. Затем строится касательная в правой точке отрезка. Находится средняя линия и переносится в левый конец отрезка. Правая точка касательной будет являться следующим приближением.
Пример2: Найти решение дифференциального уравнения на отрезке при начальном условии используя исправленный метод Эйлера. Обеспечить точность вычисления
Вводим отрезок , начальное условие (С2), (D2), (E2)(рис. 37).
Вычисляем блок А5:А15 самостоятельно.
Для заполнения ячейки В5 используется формула =C2. Для заполнения ячейки С5 используется формула =2*A5^3-B5^2. Далее заполняем ячейки D5:F5 по формулам (рис. 37).
Для заполнения ячейки В6 используется формула=B5+$E$2*(C5+F5)/2.Далее она протягивается вниз и заполняет весь столбец В, также протягиваем остальные столбцы.
Выполняем решение дифференциального уравнения исправленным методом Эйлера при
Установить, обеспечена ли требуемая точность.
Рис. 37. Численное решение дифференциального уравнения исправленным методом Эйлера
Метод Рунге-Кутта. Данный метод используется чаще остальных при решении практических задач.
Решение обыкновенного дифференциального уравнения при заданном начальном условии можно определить по итерационной формуле:
где 
Пример 3: Найти решение дифференциального уравнения на отрезке при начальном условии используя метод Рунге-Кутта. Обеспечить точность вычисления
Вводим отрезок , начальное условие (С2), (D2), (E2)(рис. 38).
Вычисляем блок А5:А15 самостоятельно.
Для заполнения ячейки В5 используется формула =C2. Для заполнения ячейки С5 используется формула =2*A5^3-B5^2. Далее заполняем ячейки D5:K5 по формулам (см. рис. 38). Обращаем внимание, что ссылки на значение 
должны быть абсолютными.
Для заполнения ячейки В6 используется формула=B5+$E$2*(C5+2*F5+2*H5+K5)/6.Далее она протягивается вниз и заполняет весь столбец В, также протягиваем остальные столбцы справа.
Рис. 38. Численное решение дифференциального уравнения методом Рунге-Кутта
Выполняем решение дифференциального уравнения методом Рунге-Кутта при
Установить, обеспечена ли требуемая точность.
Задания для самостоятельного выполнения.
Из таблицы 6 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы. Выполнить численное решение дифференциального уравнения методом Эйлера, исправленным методом Эйлера и методом Рунге-Кутта. Обеспечить точность вычисления 
Контрольные вопросы
1. Итерационная формула метода Эйлера и его геометрический смысл.
2. Погрешность формул численного решения дифференциальных уравнений.
3. Итерационная формула исправленного метода Эйлера и его геометрический смысл.
4. Итерационная формула метода Рунге-Кутта.
Линейное программирование
Процесс нахождения экстремума некоторой функции или выбор наилучшего варианта из множества возможных – это задачи оптимизации.
В линейном программировании решаются такие задачи как оптимальное управление производством; оптимальное составление смеси; оптимальное распределение ресурсов; транспортные задачи и др.
Требуется определить максимум или минимум функции 
при следующих ограничениях: 
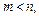
Пример: Рассмотрим задачу об оптимальном распределении ресурсов.
Для производства двух видов изделия А и В предприятие использует три вида сырья. Нормы расхода сырья каждого вида на изготовление единицы продукции представлены ниже. Требуется составить план выпуска изделий А и В, при котором прибыль от их реализации максимальна.
| Виды сырья | Нормы расхода на одно изделие | Общее количество сырья | |
| А | В | ||
| I | |||
| II | |||
| III | |||
| Прибыль |
Составим математическую модель задачи.
Пусть 
– количество изделий вида А, 
– количество изделий вида В. Тогда 
Система ограничений имеет вид:
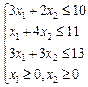
Графическое решение. Для построения области допустимых решений, перепишем неравенства системы ограничений в виде равенств.
Получили уравнения трех прямых, построим их, каждую по двум точкам (рис. 39). Прямые соответствующие ограничениям 
совпадают с осями координат.
Рис. 39. Графическое решение
Вернемся к неравенствам в системе ограничений и выделим область, которая определяет множество допустимых решений.
Построим на графике прямую (линию уровня), определяемую уравнением 
для этого зададим 
произвольное значение, удобное для вычисления. Далее переместим линию уровня параллельно самой себе до совмещения с одной из вершин многоугольника допустимых решений.
Координаты вершины определяют искомые величины и .
Заметим, что данная вершина является точкой пересечения прямых (1) и (2). Поэтому решим систему:
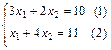
Получим 
и 
. Максимальное значение функции 
Нахождение решение с использованием пакета «Поиск решения». Встроенный пакет «Поиск решения» позволяет автоматизировать решение задач линейного программирования.
Для использования пакета оформим исходные данные (рис. 40).
Рис. 40. Исходные данные
Первоначально ввести 
и 
В ячейку D3 ввести формулу =B3*$B$2+C3*$C$2. В ячейку D5 ввести формулу =B5*$B$2+C5*$C$2 и протянуть ее вниз для заполнения столбца D, на первом этапе эти формулы дадут 0.
Вызываем команду «Поиск решения» (место ее нахождения уточняйте у преподавателя). Появится диалоговое окно (рис. 41).
Рис. 41. Диалоговое окно пакета «Поиск решения»
Заполняем поля диалогового окна (рис. 41), далее нажимаем кнопку «Параметры» и устанавливаем флажки «Линейная модель» и «Неотрицательные значения», затем нажимаем кнопку «Выполнить».
В ячейках таблицы В2: С2 появится решение задачи и 
Максимальное значение функции появится в ячейке D3 
Задания для самостоятельного выполнения.
Из таблицы 7 приложения взять исходные данные своего варианта. Вариант определяется по порядковому номеру в списке группы.
Решить задачу линейного программирования графическим методом. Задание выполняется в тетради вручную.
Решить задачу с использованием пакета «Поиск решения».
Контрольные вопросы
1. Математическая модель задачи линейного программирования.
2. Графическое решение задачи.
3. Решение задачи линейного программирования с использованием пакета «Поиск решения».
Литература
1. Бахвалов Н.С. Численные методы: 3-е изд., перераб. и доп. /Н.С.Бахвалов, Н.П.Жидков, Г.М. Кобельков – М.: БИНОМ. Лаборатория знаний, 2009. - 632 с.
2. Протасов И.Д. Лекции по вычислительной математике: учеб. пособ. /И.Д. Протасов – М.: Гелиос АРВ, 2009.
3. Исаков В.Н. Элементы численных методов: учеб. пособ. /В.Н. Исаков – М.: Академия, 2008.
4. URL: http://eqworld.ipmnet.ru/ru/library/mathematics/numerics.htm
Приложения
Таблица 1
| № п/п | Выражение | Значения параметров | ||
| А | В | С | ||
| 3,85±0,02 | 2,043±0,005 | 9,61±0,04 | |
| 1,19±0,05 | 2,3±0,1 | 5,191±0,08 | |
| 0,231±0,008 | 2,13±0,01 | 5,91±0,05 | |
| 13,28±0,02 | 2,37±0,007 | 5,13±0,01 | |
| 54,8±0,02 | 2,45±0,01 | 0,68±0,04 | |
| 0,834±0,004 | 138±0,03 | 1,84±0,01 | |
| 3,804±0,003 | 4,05±0,005 | 2,18±0,01 | |
| 2,712±0,005 | 0,37±0,02 | 13,21±0,08 | |
| 0,258±0,01 | 3,45±0,004 | 1,374±0,007 | |
| 0,323±0,005 | 3,147±0,008 | 1,78±0,05 | |
| 0,323±0,005 | 3,147±0,008 | 1,78±0,05 | |
| 4,632±0,03 | 23,3±0,04 | 11,3±0,6 | |
| 2,28±0,6 | 84,6±0,02 | 68,7±0,05 | |
| № п/п | Выражение | Значения параметров | ||
| А | В | С | ||
| 1,182±0,005 | 2,18±0,009 | 0,19±0,01 | |
| 0,95±0,01 | 2,3±0,03 | 1,195±0,005 | |
| 1,18±0,01 | 2,75±0,05 | 3,62±0,007 | |
| 1,65±0,06 | 0,09±0,04 | 13,5±0,08 | |
| 0,18±0,005 | 1,231±0,008 | 7,3±0,01 | |
| 13±0,08 | 7,1±0,02 | 0,831±0,007 | |
| 3,85±0,04 | 2,043±0,004 | 96,61±0,2 | |
|
| 13.52±0,02 | 5.1±0,03 | 9,273±0,008 | |
| 1,18±0,01 | 2,75±0,05 | 3,62±0,007 | |
| 0,323±0,005 | 3,147±0,008 | 1,78±0,05 | |
| 3,804±0,003 | 4,05±0,005 | 2,18±0,01 | |
| 1,19±0,05 | 2,3±0,1 | 5,191±0,08 | |
| 0,323±0,005 | 3,147±0,008 | 1,78±0,05 | |
| 2,28±0,6 | 84,6±0,02 | 68,7±0,05 | |
| № п/п | Выражение | Значения параметров | ||
| А | В | С | ||
|
| 0,258±0,01 | 3,45±0,004 | 1,374±0,007 | |
| 1,65±0,06 | 0,09±0,04 | 13,5±0,08 |
Таблица 2
| № п/п | Уравнение | № п/п | Уравнение |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
| 
| ||
| 
|
Таблица 3
1 
| 16 
|
2 
| 17 
|
3 
| 18 
|
4 
| 19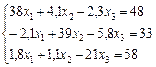 
|
5 
| 20 
|
6 
| 21 
|
7 
| 22 
|
8 
| 23 
|
9 
| 24 
|
10 
| 25 
|
11 
| 26 
|
12 
| 27 
|
13 
| 28 
|
14 
| 29 
|
15 
| 30 
|
Таблица 4
| х | 6,0 | 6,4 | 6,8 | 7,2 | 7,6 | |
| у | 1,2 | 2,45 | 4,4 | 7,2 | ||
| х | 4,5 | 10,6 | 16,7 | 22,1 | 28,3 | |
| у | 0,18 | 0,19 | 0,23 | 0,31 | 0,42 | |
| х | 5,1 | 5,4 | 5,7 | 6,0 | 6,3 | |
| у | 7,9 | 7,2 | 6,5 | 5,9 | 4,5 | |
| х | 3,1 | 9,2 | 15,3 | 21,7 | 27,2 | |
| у | 0,15 | 0,16 | 0,17 | 0,21 | 0,25 | |
| х | -1 | |||||
| у | 1,5 | 0,01 | 0,9 | 3,8 | 9,35 | |
| х | 0,15 | 0,17 | 0,19 | 0,21 | 0,25 | |
| у | 6,61 | 6,39 | 6,19 | 5,82 | ||
| х | 7,4 | 7,8 | 8,2 | 8,6 | 9,0 | |
| у | 9,01 | 6,04 | 4,24 | 3,2 | 3,01 | |
| х | 3,2 | 9,6 | 15,1 | 21,8 | 27,2 | |
| у | 0,39 | 0,45 | 0,49 | 0,52 | 0,43 | |
| х | 3,8 | 4,2 | 4,4 | 4,6 | ||
| у | 6,3 | 6,6 | 7,02 | 7,35 | 7,8 | |
| х | 1,1 | 7,2 | 13,2 | 19,1 | 22,5 | |
| у | 0,7 | 0,51 | 0,47 | 0,63 | 0,74 | |
| х | 7,8 | 8,0 | 8,2 | 8,4 | 8,6 | |
| у | 11,7 | 11,0 | 10,4 | 9,63 | 9,1 | |
| х | 0,35 | 0,41 | 0,47 | 0,51 | 0,56 | |
| у | 2,73 | 2,30 | 1,96 | 1,78 | 1,59 | |
| х | 3,45 | 3,5 | 3,55 | 3,6 | 3,65 | |
| у | 20,1 | 10,2 | 4,56 | 0,97 | 3,67 | |
| х | 4,3 | 10,2 | 16,1 | 22,8 | 28,3 | |
| у | 0,62 | 0,47 | 0,44 | 0,54 | 0,68 | |
| х | 7,6 | 8,0 | 8,4 | 8,8 | 9,2 | |
| у | 12,6 | 10,0 | 8,03 | 6,2 | 4,0 | |
| х | 0,41 | 0,46 | 0,52 | 0,60 | 0,65 | |
| у | 2,57 | 2,32 | 2,09 | 1,86 | 1,84 | |
| х | 5,45 | 5,6 | 5,75 | 5,9 | 6,05 | |
| у | 2,2 | 0,54 | 1,6 | |||
| х | 6,3 | 12,2 | 18,1 | 24,2 | 30,8 | |
| у | 0,17 | 0,28 | 0,33 | 0,27 | 0,18 | |
| х | 2,4 | 2,6 | 2,8 | 3,2 | ||
| у | 3,53 | 3,78 | 3,95 | 4,04 | 4,07 | |
| х | 0,11 | 0,15 | 0,21 | 0,29 | 0,35 | |
| у | 9,05 | 6,61 | 4,69 | 3,35 | 2,73 | |
| х | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | |
| у | 1,63 | 1,73 | 1,87 | 2,03 | 2,22 | |
| х | 0,02 | 0,08 | 0,12 | 0,17 | 0,23 | |
| у | 1,02 | 1,09 | 1,14 | 1,21 | 1,3 | |
| х | 0,15 | 0,20 | 0,25 | 0,30 | 0,35 | |
| у | 6,61 | 6,39 | 6,19 | 6,00 | 5,82 | |
| х | 1,37 | 1,38 | 1,39 | 1,4 | 1,41 | |
| у | 5,04 | 5,17 | 5,32 | 5,47 | 5,62 | |
| х | 0,4 | 0,47 | 0,51 | 0,6 | 0,67 | |
| у | 0,21 | 0,19 | 0,18 | 0,16 | 0,15 | |
| х | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | |
| у | 1,63 | 1,83 | 1,77 | 1,63 | 1,22 | |
| х | 5,45 | 5,6 | 5,75 | 5,9 | 6,05 | |
| у | 2,4 | 2,6 | 2,8 | 3,2 | ||
| х | 2,4 | 2,6 | 2,8 | 3,2 | ||
| у | 1,37 | 1,38 | 1,39 | 1,4 | 1,41 | |
| х | 0,43 | 0,48 | 0,55 | 0,62 | 0,70 | |
| у | 1,63 | 1,73 | 1,87 | 1,63 | 1,22 | |
| х | 5,45 | 5,6 | 5,75 | 5,9 | 6,05 | |
| у | 1,63 | 1,73 | 1,87 | 1,63 | 1,22 |
Таблица 5
| № п/п | y(x) | 
| 
|
| |||
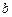
| 1,2 | 2,8 | |
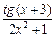
| 0,4 | ||
| 0,15 | 0,33 | |
| 0,4 | 2,2 | |
| 1,2 | 2,5 | |
| 0,8 | 1,6 | |
| 1,3 | 2,1 | |
| 1,8 | ||
| № п/п | y(x) |
|
|
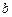
| 0,5 | 1,0 | |
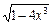
| 0,06 | ||
| 1,4 | 2,6 | |
| 0,4 | 1,8 | |
| 0,6 | 0,9 | |
| 0,02 | 0,4 | |
| 1,3 | 2,5 | |
| 1,5 | 2,7 | |
| 0,8 | 1,6 | |
| 0,4 | 0,8 | |
| 0,5 | 1,2 | |
| 0,4 | 1,2 | |
| 0,2 | 1,2 | |
| 0,6 | 1,5 | |
| 0,6 | 1,5 | |
| 0,3 | 0,8 | |
| № п/п | y(x) |
|
|
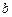
| 0,4 | 1,2 | |
| 0,02 | 0,2 | |
| 1,4 | ||
| 2,2 | ||
| 1,4 |
Таблица 6
| № п/п | 
|
|
| 
|
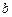
| -1 | |||
| -2 | -2 | ||
| -1 | |||
| -1 | |||
| -1 | |||
| 0,5 | 2,5 | ||
| -1 | -1 | ||
| ||||
| -1 | |||
| ||||
| 0,5 | |||
| ||||
| № п/п |
|
|
|
|
| ||||
| ||||
| ||||
| ||||
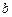
| 0,5 | |||
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
| ||||
|
| ||||
| ||||
| 0,6 | |||
| 0,7 | |||
| 0,8 |
Таблица 7
| № п/п | 
| 
| 
| 
| 
| 
| 
| 
| 
|  
| 
|
| № п/п |
|
|
|
|
|
|
|
|
|
|
|
| 0,2 | 0,1 | 1,2 | 1,5 | 0,1 | 0,3 | ||||||
| 2,3 | 1,6 | 0,2 | 0,8 | ||||||||
| 1,5 | 2,5 | ||||||||||
| 0,4 | 0,5 | 0,3 | 4,5 | 1,5 | |||||||
| 0,2 | 0,1 | 0,1 | 0,3 | 1,2 | 1,5 | ||||||
| 1,2 | 1,5 | 0,2 | 0,1 | 0,1 | 0,3 |
