1) Открыть кран К1 и К5, с помощью крана К1 стабилизировать уровень в напорном баке 1;
2) Закрыть кран К6 и отмерить отрезок времени Т, за который уровень воды в мерном баке повысится на ∆Н. Одновременно отмерить пьезометрические высоты 
и 
, а также температуру воды t; (занести данные соответственно в колонки 3,6,7 таблицы 3.2);
3) Опыт необходимо повторить несколько раз, изменяя каждый раз с помощью крана К5 расход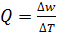 
, где 
, где S – площадь основания мерного бака; Н1 и Н2 – уровни воды в баке до измерения и через промежуток времени Т (занести данные в колонки 2,4 таблицы 3.2);
4) При проведении измерений и вычислений длину рабочей части трубы принимаем L=3100 мм, а диаметр трубы d=20 мм;
5) Определить по формуле (3.2) экспериментальные значения 
и занести результаты в колонку 8 таблицы 3.2.
6) По формуле (3.3) определить экспериментальные значения 
и и занести результаты в колонку 9 таблицы 3.2
7) Определить теоретическое значение коэффициента 
в зависимости от зоны гидравлических сопротивлений по формулам (3.5÷3.7) и занести в колонку 12 таблицы 3.2. Для определения зоны гидравлических сопротивлений определить число Рейнольдса (см. формулу 2.1) и сравнить его с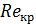 
=2300 и значением относительной шероховатости поверхности трубы. Если вычисленное значение 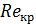удовлетворяет неравенству (3.5), то 
определяется по формуле 3.6 и т.д. Полученные результаты занести в колонки 10,11 и 12 таблицы 3.2
| N п/п | Объем воды в мерном баке,W(м3) | Время наполнения бака,  Т(с)
| Расход, Q(м3./с) | Средняя скорость в сечении, V(м/c) | Пьезометрические высоты (м) | Потери энергии, hl (м) | Коэффициент Дарси из формулы (3.3) | Число Рейнольдса Re | Зона гидравлического сопротивления | Коэффициент Дар-си из эмпирической формулы (3.4÷3.6) | Погрешность (%) | |
| P1/pg | P2/pg | |||||||||||
8) Относительную погрешность экспериментальных значений коэффициента Дарси 
вычислить по формуле 
и результаты занести в колонку 13 таблицы (3.2)
Таблица 3.2
Содержание отчета
1. Цель работы;
2. Краткие теоретические сведения;
3. Схема лабораторного стенда (см. рис. 3.2);
4. Заполненную таблицу 3.2 результатами измерений и вычислений;
5. Расчетные формулы с подстановкой числовых данных и результаты расчетов;
6. Выводы по результатам исследований.
Контрольные вопросы
а) От каких параметров потока зависят потери на трение по длине при ламинарном течении жидкости?
б) С чем связано разделение турбулентного потока на «области сопротивлений»?
в) От каких параметров зависят потери по длине при турбулентном движении жидкости?
г) Какова структура турбулентного потока?
Библиографический список
1. Гидравлика, гидромашины, гадроприводы / Т.М. Башта, С.С. Руднев, Б.Б. Некрасов и др. - М: Машиностроение, 1982. - 423с.
2. А.А. Угинчус. Гидравлика и гидравлические машины – изд. 4, перераб. и доп -Изд-во Харьковского ун-та, 1970. — С
3. Большаков В. А. и др. Справочник по гидравлике. - К.: Вища школа, 1984 - 343 с
4. Вакина Б.В., Денисенко И.Д., Столяров А.Л. Машиностроительная гидравлика Примеры расчетов. - К.: Вища школа 987. - 208 с.
4. Лабораторная работа №4.
«Экспериментальное исследование
коэффициентов местных гидравлических сопротивлений»
Цель работы: экспериментально установить коэффициенты местных гидравлических сопротивлений и сравнить их значения с табличными (справочными).
Теоретический раздел
Общие положения
Местные сопротивления – это сравнительно короткие участки труб, в границах которых возникают – нарушения равномерных потоков из-за наличия помех – запорных устройств, поворотов, изменений диаметра трубы и т.д.
Потери энергии на преодоление местных гидравлических сопротивлений определяются по формуле Вейсбаха:
, (4.1)
где 
– коэффициент местного сопротивления, который при турбулентном режиме зависит только от вида сопротивления и его относительных размеров. Коэффициент местного сопротивления определяют на основе экспериментальных исследований. Значение коэффициентов можно найти в справочниках по гидравлике. В некоторых случаях их можно вычислить по теоретическим или полутеоретическим формулам. Например, для резкого расширения трубы:
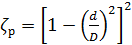(4.2)
для резкого сужения
(4.3)
Значения некоторых других коэффициентов местных сопротивлений () можно найти в таблице 4.1.
Таблица 4.1 – Коэффициенты местных сопротивлений для различных видов сопротивлений
| Вид местного сопротивления | Значения коэффициента
|
| Вход в трубу | 0,5 |
| Всасывающий клапан | 6…12 |
| Колено | 1,2 |
Плавный поворот на 
| |
| Вентиль (открытый) | 6…9 |
| Выход из трубы |
Следует отметить, что при ламинарном режиме коэффициенты местных сопротивлений зависят не только от их формы и относительных размеров, но и от числа Рейнольдса:
(4.4)
где А – установленный экспериментально безразмерный коэффициент. При выполнении этой лабораторной работы определяют коэффициенты только для турбулентного режима, потому что ламинарный режим наблюдается сравнительно редко.
Лабораторный стенд (см. рис. 4.1) состоит из напорного бака 1, трубы 2 с различными местными сопротивлениями, мерного бака 3. До и после каждого местного сопротивления установлены гидродинамические трубки.
Рисунок 4.1 – Схема лабораторного стенда
